Определение и примеры метрических пространств, страница 18

Теорема Арцела имеет многочисленные приложения. Продемонстрируем ее применение на примере следующей теоремы существования для обыкновенных дифференциальных уравнений с непрерывной правой частью.

Теорема 2 (Пеано). Пусть дано дифференциальное уравнение

Если функция f(x, у) непрерывна в некоторой замкнутой ограниченной области G, то через каждую внутреннюю точку  этой области проходит по крайней мере одна интегральная кривая данного уравнения.

Доказательство. Так как f(x, у)непрерывна в замкнутой области, то она ограничена:

Проведем через точку  прямые с угловыми коэффициентами М и – М. Проведем, далее, вертикальные прямые x = а и х = b так, чтобы отсекаемые ими два треугольника с общей вершиной  целиком лежали внутри области G.

Построим теперь для данного уравнения так называемые ломаные Эйлера следующим образом: проведем из точки  прямую с угловым коэффициентом  На этой прямой возьмем некоторую точку  и проведем через нее прямую с угловым коэффициентом  На этой прямой возьмем точку  проведем через нее прямую с угловым коэффициентом  и т.д. Рассмотрим теперь последовательность ломаных Эйлера  проходящих через точку  таких, что длина наибольшего из звеньев линии  стремится к нулю при  Пусть  — функция, график которой есть линия  Функции  обладают следующими свойствами:

1) они определены на одном и том же отрезке [а, b],

2) они ограничены в совокупности,

3) они равностепенно непрерывны.

На основании теоремы Арцела из последовательности  можно выбрать равномерно сходящуюся подпоследовательность. Пусть это будет подпоследовательность

Положим  Ясно, что  Остается проверить, что  удовлетворяет на отрезке [а, b] данному дифференциальному уравнению. Для этого нужно показать, что для любого

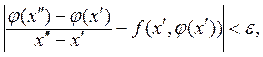
если только величина  достаточно мала. Для доказательства этого в свою очередь достаточно установить, что при достаточно больших k

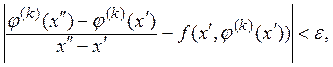
как только разность  достаточно мала.

Так как f(x, у) непрерывна в области G, то для любого  можно найти такое  что

если

Совокупность точек  удовлетворяющих этим двум неравенствам, представляет собой некоторый прямоугольник Q. Пусть теперь K настолько велико, что для всех k > К

и все звенья ломаной  имеют длину меньше  Тогда при  все ломаные Эйлера  для которых k > К, целиком лежат внутри Q.

Далее, пусть  — вершины ломаной  причем

(мы для определенности считаем  аналогично рассматривается случай  Тогда

Отсюда при  получаем:

Суммируя эти неравенства, получаем:

что и требовалось доказать.

Полученное решение  вообще говоря, не будет единственным решением уравнения  проходящим через точку

§18. Компакты

В § 16 мы назвали множество М, лежащее в метрическом пространстве R, компактным, если из всякой последовательности его элементов можно выбрать подпоследовательность, сходящуюся к некоторому

При этом сама предельная точка х может принадлежать, но может и не принадлежать множеству М. Если из всякой последовательности элементов из М можно выбрать подпоследовательность, сходящуюся к некоторому х, принадлежащему М, то множество М называется компактным в себе. Для самого пространства R (как, впрочем, и для всех его замкнутых подмножеств) понятия компактности и компактности в себе совпадают. Компактное метрическое пространство кратко называется компактом.

Поскольку компактность в себе некоторого множества есть внутреннее свойство этого множества, не зависящее от того, в каком именно объемлющем метрическом пространстве оно рассматривается, естественно ограничиться изучением компактов, т.е. каждое такое множество рассматривать просто как отдельное метрическое пространство.

Теорема 1. Для того чтобы компактное в метрическом пространстве R множество М было компактом, необходимо и достаточно, чтобы М было замкнуто в R.

Доказательство. Необходимость. Пусть М не замкнуто, тогда в М найдется последовательность  сходящаяся к точке  Но тогда эта последовательность не может содержать подпоследовательности, сходящейся к какой-либо точке  т. е. М не может быть компактом.