Другие предметы \ Функциональный анализ

Определение и примеры метрических пространств, страница 11

Из аксиомы треугольника непосредственно следует, что всякая сходящаяся последовательность — фундаментальная. Действительно, если  сходится к х, то для данного  можно найти такое целое число  что  для всех  Тогда  для любых  и

Определение 1. Если в пространстве R любая фундаментальная последовательность сходится, то это пространство называется полным.

Примеры. Все пространства, рассмотренные в § 8, за исключением указанного в примере 7, являются полными. Действительно:

1. В пространстве, состоящем из изолированных точек (пример 1 § 8), фундаментальными являются только те последовательности, в которых, начиная с некоторого номера, повторяется все время одна и та же точка. Ясно, что всякая такая последовательность сходится, т. е. это пространство полно.

2. Полнота пространства R1— совокупности действительных чисел — известна из анализа.

3. Полнота евклидова пространства  непосредственно вытекает из полноты R1. Действительно, пусть  — фундаментальная последовательность; это означает, что для каждого  найдется такое  что

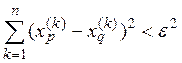
при всех р, q, больших чем N. Тогда для каждого

для всех р, q > N, т. е.  — фундаментальная числовая последовательность. Положим,

и

Тогда, очевидно,

4. Полнота пространства  доказывается совершенно аналогично.

5. Докажем полноту пространства  Пусть  — некоторая фундаментальная последовательность в  Это означает, что для каждого  существует такое N, что  при п, т > N для всех  Отсюда вытекает, что последовательность  равномерно сходится, ее предел есть некоторая непрерывная функция x(t), причем

для всех t и для всех п, больших чем некоторое N, а это и означает, что  сходится к x(t) в смысле метрики пространства

6. Пространство l2. Пусть  где

— фундаментальная последовательность в l2.

Для любого  найдется такое N, что

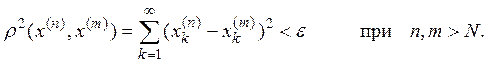                      (1)

Отсюда следует, что при любом k

т.е. при каждом k последовательность действительных чисел  сходится. Положим  Обозначим через х последовательность  Нужно показать, что:

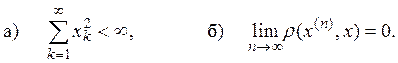
Для этого неравенство (1) запишем в виде

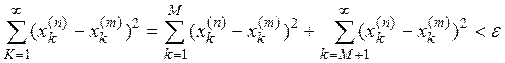
(M произвольно). Так как каждая из этих двух сумм неотрицательна, то каждая из них не больше  Следовательно,

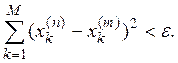
Зафиксируем в этом неравенстве т и перейдем к пределу при

Получим:

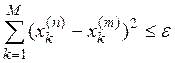
Так как это неравенство верно при любом М, то в нем можно перейти к пределу при  Получим:

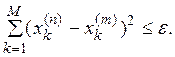
Из полученного неравенства и сходимости ряда 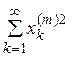 следует сходимость ряда  следовательно, х есть элемент из l2. Далее, так как  произвольно мало, то это неравенство означает, что

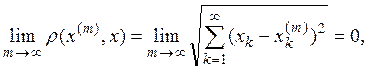
т.е.

7. Легко убедиться в том, что пространство  полно. Например, последовательность непрерывных функций

фундаментальная, но она не сходится ни к какой непрерывной функции (она сходится в смысле среднего квадратичного уклонения к разрывной функции, равной  при t < 0,  при t > 0 и 0 при t = 0).

Упражнение. Доказать, что пространство всех ограниченных последовательностей (§ 8, пример 8) полно.

В анализе широко используется так называемая лемма о вложенных отрезках. В теории метрических пространств аналогичную роль играет следующая теорема, называемая принципом вложенных сфер.

Теорема 1. Для того чтобы метрическое пространство R было полным, необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга замкнутых сфер, радиусы которых стремятся к нулю, имела непустое пересечение.

Доказательство. Необходимость.  Пусть пространство R полно и пусть  — последовательность вложенных друг в друга замкнутых сфер. Пусть  — диаметр сферы  По условию  Обозначим через  центр сферы  Последовательность  — фундаментальная. Действительно, если  то, очевидно,  Так как R полно, то  существует. Положим,

тогда  Действительно, сфера  содержит все точки данной последовательности, за исключением, может быть, точек  Таким образом, х является предельной точкой для каждой сферы  Но так как — замкнутое множество, то  для всех n.

Скачать файл