Определение и примеры метрических пространств, страница 14

В частности, условие сжатости выполнено, если на сегменте [а, b]

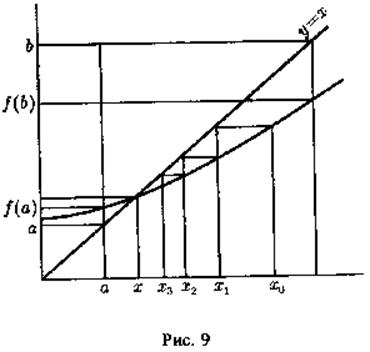
Для иллюстрации на рис. 9 и 10 изображен ход последовательных приближений в случае  и в случае

В случае, если мы имеем дело с уравнением вида F(x) = 0, причем F(a) < 0, F(b) > 0 и  на [а, b], то распространенный метод нахождения его корня заключается в том, что полагают  и ищут решение уравнения х = f(x), равносильного F(x) = 0. Действительно, так как  то  и нетрудно  подобрать так, чтобы можно было действовать методом последовательных приближений.

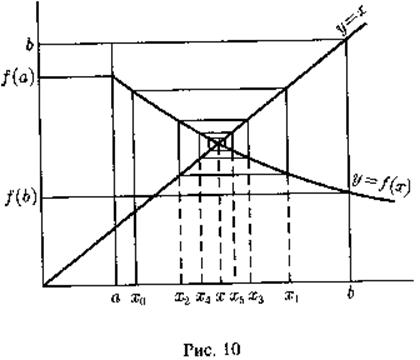
2. Рассмотрим отображение у = Ах пространства  в себя, задаваемое системой линейных уравнений

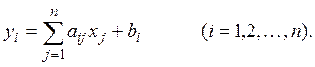
Если Ax есть сжатое отображение, то мы можем применить метод последовательных приближений к решению уравнения х = Ах.

При каких же условиях отображение А будет сжатым? Ответ на этот вопрос зависит от выбора метрики в [6]

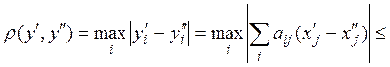
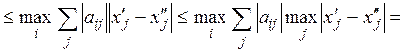
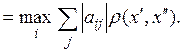
Отсюда условие сжатости

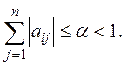 (2)

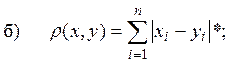
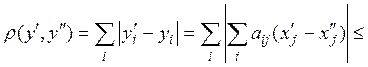
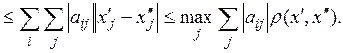
Отсюда условие сжатости

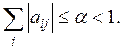                                                          (3)

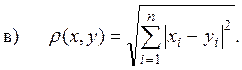
На основании неравенства Коши-Буняковского

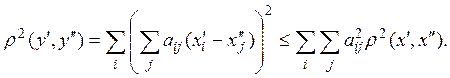
Отсюда условие сжатости

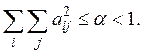                                                       (4)

Таким образом, в случае, если выполнено одно из условий (2)-(4), то существует одна и только одна точка  такая, что 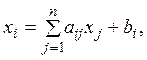[7] причем последовательные приближения к этому решению имеют вид:

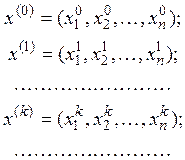
где

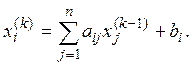
Каждое из условий (2)-(4) является достаточным для того, чтобы отображение  было сжатым. Относительно условия (2) можно было бы доказать, что оно является и необходимым для сжатости отображения у = Ах (в смысле метрики а).

Ни одно из условий (2)-(4) не является необходимым для применимости метода последовательных приближений. Можно построить примеры, в которых какое-либо из этих условий выполнено, а остальные два нет.

Если  (в этом случае все три условия выполнены), то метод последовательных приближений применим.

Если  (в этом случае все три суммы равны 1), то, как легко видеть, метод последовательных приближений, вообще говоря, неприменим.

§ 15. Применение принципа сжатых отображений в анализе

В предыдущем параграфе были указаны некоторые простейшие примеры применения принципа сжатых отображений в одномерном и в п-мерном пространствах. Однако наиболее существенны для анализа применения принципа сжатых отображений в бесконечномерных функциональных пространствах. Ниже мы покажем, как с помощью этого принципа можно получить теоремы существования и единственности решения для некоторых типов дифференциальных и интегральных уравнении.

I. Пусть дано дифференциальное уравнение

                                                            (1)

с начальным условием

                                                            (2)

причем f(x, y) определена и непрерывна в некоторой плоской области G, содержащей точку  и удовлетворяет условию Липшица по у:

Докажем, что тогда на некотором сегменте  существует, и притом только одно, решение  уравнения (1), удовлетворяющее начальному условию (2) (теорема Пикара).

Уравнение (1) вместе с начальными условиями (2) эквивалентно интегральному уравнению

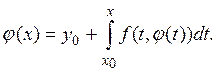                                                (3)

В силу непрерывности функции f(x, у) имеем:  в некоторой области  содержащей точку  Подберем теперь d > 0 так, чтобы выполнялись условия:

1)  если

2) Md < 1.

Через С* обозначим пространство непрерывных функций  определенных на сегменте  и таких, что  метрикой

Легко видеть, что С* есть полное пространство[8]. Рассмотрим отображение  определяемое формулой

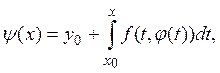
где  Это — сжатое отображение полного пространства С* в себя. Действительно, пусть  Тогда

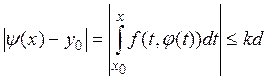
и, следовательно,  Кроме того,

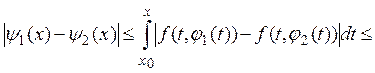
Так как Md < 1, то отображение А сжатое.

Отсюда вытекает, что операторное уравнение  (а следовательно, и уравнение (3)) имеет одно и только одно решение.

II. Пусть дана система дифференциальных уравнений

                                 (4)

с начальными условиями

причем функции  определены и непрерывны в некоторой области G пространства  содержащей точку  и удовлетворяют условию Липшица