Определение и примеры метрических пространств, страница 22

Верхним пределом  функции f(х), в точке  называется  Нижним пределом  называется

Разность  называется колебанием функции  в точке  Легко видеть, что для непрерывности f(х) в точке хо необходимо и достаточно, чтобы  т. е. чтобы

Для любой f(х) функция  полунепрерывна сверху, а функция  полунепрерывна снизу. Это легко вытекает из определения верхнего и нижнего предела.

Рассмотрим некоторые важные примеры полунепрерывных функционалов.

Пусть f(х) — действительная функция действительного переменного. Для любых действительных а и b, таких, что f(х) определена на [а, b], определим полную вариацию функции f(х) на [а, b] как функционал

где и верхняя грань берется по всевозможным разбиениям сегмента [а, b].

Для монотонной функции  Для кусочно-монотонной функции  есть сумма абсолютных величин приращений на сегментах монотонности. Для таких функций  достигается при некотором разбиении.

Докажем, что функционал  полунепрерывен снизу в пространстве М всех ограниченных функций действительного переменного с метрикой  (очевидно, что С есть подпространство пространства М), т. е. что для любых f и  существует такое  что  при

Возьмем такое разбиение сегмента [а, b], чтобы

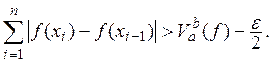
Пусть  Тогда, если  то

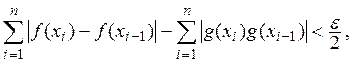
и, следовательно,

В случае  теорема остается справедливой, так как тогда для любого Н существует такое разбиение сегмента [a, b], что

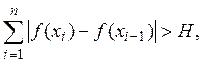
а  можно подобрать так, чтобы

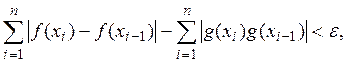
и тогда  т. е.

Функционал  не непрерывен, как это легко видеть из следующего примера. Пусть  Тогда

но

Функции, для которых  называются функциями ограниченной вариации. О свойствах таких функций читатель может прочесть в книге Александрова и Колмогорова «Введение в теорию функций действительного переменного», гл. 7, § 7.

Определим длину кривой  как функционал

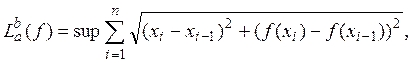
где верхняя грань берется по всевозможным разбиениям сегмента [а, b]. Этот функционал определен на всем пространстве М. Для непрерывных функций он совпадает со значением предела

Наконец, для функций с непрерывной производной его можно записать в виде

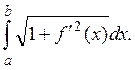
Функционал  полунепрерывен снизу в М, что доказывается так же, как и в случае функционала

На полунепрерывные функции обобщаются установленные выше теоремы 2 и 3.

Теорема 2а. Полунепрерывная снизу (сверху) конечная функция ограничена снизу (сверху) на компакте.

Действительно, пусть f конечна, полунепрерывна снизу и  Тогда существует последовательность  такая, что

Выбираем подпоследовательность  Тогда в силу полунепрерывности снизу  что противоречит допущению о конечности f(x). Аналогично доказывается теорема и для случая полунепрерывной сверху функции.

Теорема 3а. Полунепрерывная снизу (сверху) конечная функция достигает на компакте своей нижней (верхней) грани.

Пусть функция f полунепрерывна снизу. Тогда по теореме 2 она имеет конечную нижнюю грань и существует последовательность  такая, что  Выберем подпоследовательность  Тогда  так как предположение  противоречит полунепрерывности снизу.

Аналогично доказывается теорема и для случая полунепрерывной сверху функции.

Пусть К — компактное метрическое пространство, а  — пространство непрерывных действительных функций на К с расстоянием  Тогда имеет место

Теорема 4. Для компактности множества  необходимо и достаточно, чтобы функции, принадлежащие D, были равномерно ограничены и равностепенно непрерывны. (Теорема Арцела для непрерывных функций на любом компакте.)

Достаточность вытекает из общей теоремы 7 § 18. Необходимость доказывается так же, как и при доказательстве теоремы Арцела (см. § 17).

§ 20. Непрерывные кривые в метрических пространствах

Пусть задано непрерывное отображение

отрезка