Определение и примеры метрических пространств, страница 2

метрическое пространство и М – любое подмножество в X, то М с той же функцией  но уже считающейся определенной только для х и у из М, тоже представляет собой метрическое пространство; оно называется подпространством пространства R.

(1) В определении метрического пространства можно было бы ограничиться двумя аксиомами для  а именно:

1)  

тогда и только тогда, когда х = у;

2)

для любых х, у, z.

Отсюда уже вытекает, что

3)

4)

и, следовательно, аксиома 2 может быть записана в виде

2')

(2). Множество Dⁿупорядоченных групп по п действительных чисел с расстоянием

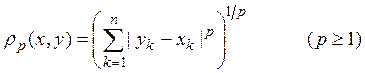
также представляет собой метрическое пространство, которое мы обозначим  Здесь справедливость аксиом 1 и 2 опять-таки очевидна. Проверим аксиому 3. Пусть

точки из  Положим, как и в примере 3,

тогда неравенство

принимает вид

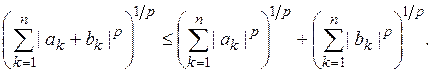                            (7)

Это так называемое неравенство Минковского. При р = 1 неравенство Минковского очевидно (модуль суммы не превосходит суммы модулей), поэтому мы можем ограничиться рассмотрением случая р > 1.

Для доказательства неравенства (7) при р > 1 мы установим предварительно так называемое неравенство Гельдера:

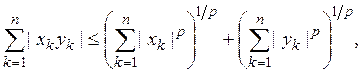                                   (8)

где число q определяется условием

                                                        (9)

Заметим, что неравенство (8) однородно в том смысле, что если оно выполнено для каких-либо двух векторов

то оно выполнено и для любых двух векторов  и  где  и  — произвольные числа. Поэтому неравенство (8) достаточно доказать для того случая, когда

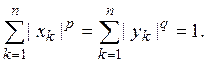                                          (10)

Итак, нам нужно доказать, что если выполнено условие (10), то

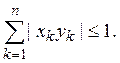                                                 (11)

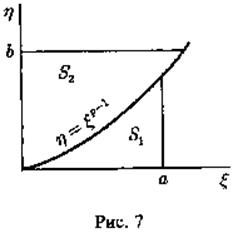Рассмотрим на плоскости  кривую, определяемую уравнением  или что то же самое, – уравнением  (см. рис. 7). Из чертежа ясно, что при любом выборе положительных значений а и b будет  Вычислим площади S₁и S₂. Получаем

Таким образом

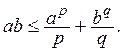
Полагая  и суммируя по k от 1 до п, получим, учитывая (9) и (10),

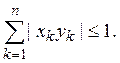
Неравенство (11), а следовательно, и общее неравенство (8) доказаны. При р = 2 неравенство Гельдера (8) переходит в неравенство Коши - Буняковского(1).

Перейдем теперь к доказательству неравенства Минковского. Для этого рассмотрим тождество

Полагая в написанном тождестве  суммируя по k от 1 до п, получим

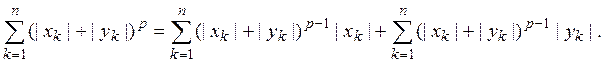
Применяя теперь к каждой из двух сумм, стоящих справа, неравенство Гельдера и учитывая, что  получим

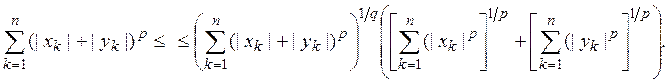
Деля обе части этого неравенства на

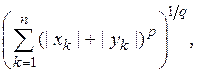
получим

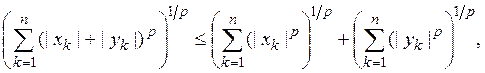
откуда сразу следует неравенство (7). Тем самым установлена аксиома треугольника в пространстве

(3) Можно показать, что метрика

введенная в примере 4, может быть определена следующим образом:

(4) Из неравенства

установленного в примере (2), легко выводится и интегральное неравенство Гельдера

справедливое для любых функций x(t) и y(t), для которых стоящие справа интегралы имеют смысл. Отсюда в свою очередь получается интегральное неравенство Минковского

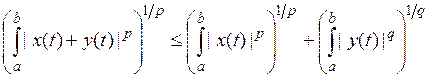
(5) Укажем еще один интересный пример метрического пространства. Его элементами являются всевозможные последовательности действительных чисел

такие, что

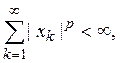
где  — некоторое фиксированное число, а расстояние определяется

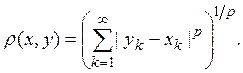                                        (12)

Это метрическое пространство мы обозначим l_p.

В силу неравенства Минковского (7) имеем при любом п

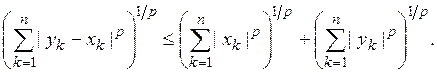
Так как по предположению ряды

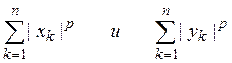
сходятся, то, переходя к пределу при  получим

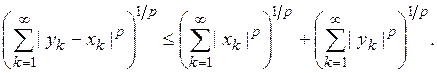(13)

и ряд слева также сходится. Таким образом, доказано, что формула (12), определяющая расстояние в l_p действительно имеет смысл для любых  Одновременно неравенство (13) показывает, что в l_p выполнена аксиома треугольника. Остальные аксиомы очевидны.

§ 9. Сходимость последовательностей. Предельные точки

В § 9-11 мы установим некоторые основные понятия, которыми нам неоднократно придется пользоваться в дальнейшем.

Открытой сферой  в метрическом пространстве R мы будем называть совокупность точек  удовлетворяющих условию