Определение и примеры метрических пространств, страница 4

Следующая теорема устанавливает тесную связь между понятиями точки прикосновения и предельной точки, с одной стороны, и понятием продела — с другой.

Теорема 5. Для того чтобы точка х была точкой прикосновения множества М, необходимо и достаточно, чтобы существовала последовательность  точек множества М, сходящаяся к х; для того чтобы точка х была предельной для М — необходимо и достаточно, чтобы существовала сходящаяся к х последовательность, состоящая из попарно различных точек множества М.

Доказательство. Необходимость. Если x — точка прикосновения множества М, то в каждой ее окрестности  содержится хотя бы одна точка  Эти точки образуют последовательность, сходящуюся к х. Если точка х — предельная для М, то в каждой окрестности  можно найти точку  отличную от всех  (так как число таких точек конечно). Точки попарно различны и образуют последовательность, сходящуюся к х.

Достаточность очевидна.

Пусть А и В — два множества в метрическом пространстве R. Множество А называется плотным в В, если  В частности, множество А называется всюду плотным (в R), если его замыкание [А] совпадает со всем пространством R. Например, множество рациональных чисел всюду плотно на числовой прямой.

Примеры пространств, имеющих всюду плотное счетное множество[2]. Рассмотрим те же самые примеры, которые указаны в § 8.

1. Пространство, описанное в примере 1 §8, сепарабельно тогда и только тогда, когда оно состоит из счетного числа точек. Это непосредственно вытекает из того, что в этом пространстве [М] = М для любого множества М.

Все пространства, перечисленные в примерах 2-7 § 8, сепарабельны. Укажем в каждом из них по счетному всюду плотному множеству, предоставляя детали доказательств читателю.

2. Рациональные точки.

3. Совокупность векторов с рациональными координатами.

4. Совокупность векторов с рациональными координатами.

5. Совокупность всех многочленов с рациональными коэффициентами.

6. Совокупность последовательностей, в каждой из которых все члены рациональны, и лишь конечное (но произвольное) число их отлично от нуля.

7. Совокупность всех многочленов с рациональными коэффициентами.

Пространство ограниченных последовательностей (пример 8 § 8) не сепарабельно. Действительно, рассмотрим всевозможные последовательности, состоящие из нулей и единиц. Они образуют множество мощности континуума (так как каждую из них можно сопоставить с двоичным разложением некоторого действительного числа, заключенного между 0 и 1). Расстояние между двумя такими точками, определяемое формулой (6) § 8, равно 1. Окружим каждую из этих точек сферой радиуса  Эти сферы не пересекаются. Если некоторое множество всюду плотно в рассматриваемом пространстве, то в каждой из указанных сфер должно содержаться хотя бы по одной точке из этого множества, и, следовательно, оно не может быть счетно.

(1) Пусть А — некоторое множество в метрическом пространстве R и х — точка этого же пространства. Расстоянием от точки х до множества А называется число

Если  то  однако из того, что  не следует, что  Из определения точки прикосновения непосредственно получаем  в том и только в том случае, если х есть точка прикосновения множества А.

Таким образом, замыкание [А] множества А может быть определено как совокупность всех тех точек, расстояние которых от множества А равно нулю.

(2) Аналогично можно определить расстояние между двумя множествами. Если А, В — два множества в R, то

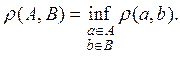
Если  то  обратное, вообще говоря, неверно.

(3) Если А — множество в метрическом пространство R, то совокупность А' его предельных точек называется его производным множеством.

В то время как, применяя к [М] еще раз операцию замыкания, мы всегда получим снова [М], равенство (М')' = М', вообще говоря, не имеет места. Действительно, возьмем, например, множество А точек вида  на числовой прямой. Его производное множество А' состоит из единственной точки 0, а множество А" = (А')' будет уже пустым множеством. Если мы рассмотрим на прямой множество В всех точек вида  то  есть точка 0, а B'" — пустое множество.