В предыдущей главе мы установили, что пространства L2 (в случае сепарабельной меры) и l2 изоморфны, т. е. по существу представляют собой две различные реализации одного и того же пространства. Это пространство, называемое обычно гильбертовым пространством, играет важную роль в анализе и его приложениях. Часто бывает удобно не связывать себя заранее той или иной реализацией этого пространства, а определять его аксиоматически, как это делается, например, в линейной алгебре по отношению к n-мерному евклидову пространству.
Определение 1. Совокупность Н элементов 
произвольной
природы называется (абстрактным) гильбертовым пространством, если выполнены
следующие условия:
I. H есть линейное пространство.
II. В Н определено скалярное произведение элементов, т. е. каждой паре элементов f и g поставлено в соответствие число f, g так, что
1) ( f , g ) = ( g , f ),
2) 
3)
4)
Иначе
говоря, условия I и II означают, что Н – евклидово пространство. Число |
называется нормой элемента f.
III. Пространство Н полно
в смысле метрики 
IV. Пространство Н бесконечномерно, т.е. для любого натурального п в Н можно найти п линейно независимых векторов.
V. Пространство Н сепарабельно[1], т.е. в нем существует счетное всюду плотное множество.
Легко указать примеры пространств, удовлетворяющих всем перечисленным аксиомам. Таково рассмотренное нами в гл. II пространство l2. Действительно, оно представляет собой евклидово пространство, бесконечномерное, так как, например, его элементы
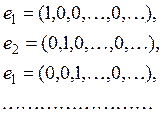
линейно независимы; его полнота и сепарабельность были доказаны в гл. II, §§ 9 и 13. Этим же аксиомам удовлетворяет и изоморфное ему пространство L2 функций, квадрат которых интегрируем по некоторой сепарабельной мере.
Справедливо следующее утверждение: все гильбертовы пространства изоморфны между собой.
Для доказательства этого факта достаточно, очевидно, установить, что всякое гильбертово пространство изоморфно координатному пространству l2. Это последнее утверждение доказывается по существу теми же рассуждениями, что и изоморфизм пространств L2и l2, а именно:
1. На абстрактное гильбертово пространство переносятся без всяких изменений те определения ортогональности, замкнутости и полноты, которые были введены в § 53 для элементов пространства L2.
2. Выбрав в гильбертовом пространстве Н счетное всюду плотное множество и применив к нему процесс ортогонализации, описанной (применительно к L2) в § 53, мы построим в Н полную ортогональную нормированную систему элементов, т. е. систему
(1)
удовлетворяющую условиям:
а)
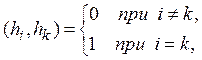
б) линейные комбинации элементов системы (1) всюду плотны в Н.
3. Пусть f —
произвольный элемент из Н. Положим 
Тогда
ряд 
сходится, и 
любой
полной ортогональsной нормированной системы 
и
любого элемента 
4. Пусть опять – некоторая полная ортогональная
нормированная система элементов в Н. Какова бы ни была
последовательность чисел
удовлетворяющая условию
в Н существует такой элемент что
и
5. Из сказанного видно, что можно осуществить изоморфное отображение Н на l2положив:
где
и
– произвольная полная ортогональная нормированная система в Н.
Детали доказательств читателю рекомендуется провести самостоятельно по образцу § 53-55.
В соответствии с общими определениями § 21 гл. III, линейным
многообразием в Н мы назовем такую совокупность L элементов из Н, что если 
то 
для любых чисел 
и
Замкнутое линейное многообразие называется
подпространством.
Приведем некоторые примеры подпространств гильбертова пространства.
1. Пусть h — произвольный элемент из Н. Совокупность всех
элементов 
ортогональных к h, образует в Н подпространство.
2. Пусть Н реализовано как l2, т. е. его элементы суть последовательности 
чисел, такие, что 
Элементы,
удовлетворяющие условию 
образуют подпространство.
3. Пусть Н реализовано как пространство L2 всех функций с суммируемым квадратом на некотором отрезке
[а, b], и пусть а < с < b. Обозначим 
совокупность всех функций из Н, тождественно
равных нулю на отрезке [a, с]. представляет собой подпространство
пространства Н. Если 
то 
при этом 
Таким
образом, здесь мы получаем континуум вложенных друг в друга подпространств пространства
Н. Каждое из этих подпространств (за исключением, разумеется, 
)бесконечномерно и изоморфно всему
пространству Н.
Читателю рекомендуется проверить, что указанные в примерах 1-3 совокупности векторов действительно являются подпространствами.
Всякое подпространство гильбертова пространства является или конечномерным евклидовым пространством, или само представляет собой гильбертово пространство. Действительно, справедливость аксиом I—III для каждого такого подпространства очевидна, а справедливость аксиомы V вытекает из следующей леммы.
Лемма. Из существования счетного всюду плотного множества в
метрическом пространстве R вытекает существование счетного всюду плотного множества в
любом его подпространстве 
Доказательство. Пусть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
