Абстрактное гильбертово пространство. Интегральные уравнения с симметричным ядром, страница 4

согласно (2),

где А – самосопряженный линейный оператор.

Так как соответствие между симметричными билинейными функционалами и квадратичными функционалами взаимно однозначно[4], то и соответствие между квадратичными функционалами и самосопряженными линейными операторами тоже взаимно однозначно.

§ 59. Вполне непрерывные самосопряженные операторы в h

В гл. IV ч. I было введено понятие вполне непрерывного линейного оператора, действующего в некотором банаховом пространстве Е. В этом параграфе мы, ограничиваясь лишь самосопряженными вполне непрерывными операторами, действующими в гильбертовом пространстве, дополним те факты, которые были установлены для произвольных вполне непрерывных операторов.

Напомним, что оператор А мы назвали вполне непрерывным, если он каждое ограниченное множество переводит в компактное. Поскольку  т. е. Н является сопряженным к сепарабельному, в нем все ограниченные множества (и только они) слабо компактны; поэтому в случае гильбертова пространства определение полной непрерывности можно сформулировать так.

Оператор А, действующий в гильбертовом пространстве Н, называется вполне непрерывным, если он всякое слабо компактное множество переводит в компактное (по норме).

В гильбертовом пространстве это равносильно тому, что оператор А всякую слабо сходящуюся последовательность переводит в сильно сходящуюся.

В этом параграфе мы установим следующую основную теорему, представляющую собой обобщение на самосопряженные вполне непрерывные операторы теоремы о приведении матрицы самосопряженного линейного преобразования в n-мерном пространстве к диагональной форме.

Теорема 1. Для любого вполне непрерывного самосопряженного линейного оператора А в гильбертовом пространстве Н существует ортогональная нормированная система  собственных векторов, отвечающих собственным значениям  такая, что каждый элемент  записывается единственным образом в виде  где вектор  удовлетворяет условию  при этом

и

Для доказательства этой основной теоремы нам понадобятся следующие вспомогательные утверждения:

Лемма 5. Если  слабо сходится к  самосопряженный линейный оператор А вполне непрерывен, то

Доказательство.

Но

и

и так как числа  ограничены, а  то

что и требовалось доказать.

Лемма 6. Если функционал

– ограниченный самосопряженный линейный оператор, достигает на единичной сфере максимума в точке  то из

вытекает, что

Доказательство. Очевидно,  Положим

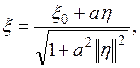
где a – произвольное число. Из  следует, что

Так как

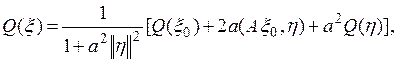
то при малых а

Из последнего равенства ясно, что если  то а можно выбрать так, что  что противоречит условию леммы.

Из леммы 2 непосредственно вытекает, что если  достигает максимума при  то  есть собственный вектор оператора А.

Доказательство теоремы. Будем строить элементы  по индукции, в порядке убывания абсолютных величин соответствующих им собственных значений:

Для построения элемента  рассмотрим выражение  и докажем, что оно на единичной сфере достигает максимума. Пусть

и  – такая последовательность, что  и

Так как единичная сфера в H слабо компактна, то из  можно выбрать подпоследовательность, слабо сходящуюся к некоторому элементу . При этом, согласно теореме 1 §58,  а в силу леммы 1

Элемент  мы и примем за  Ясно что  в точности равняется 1. При этом

откуда

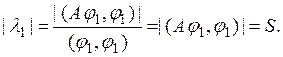
Пусть теперь собственные векторы

отвечающие собственным значениям

уже построены. Рассмотрим функционал

на совокупности элементов, принадлежащих

(т.е. ортогональных ) и удовлетворяющих условию  представляет собой подпространство, инвариантное относительно А (так как М  инвариантно и А самосопряжен). Применяя к М_п проведенные выше рассуждения, получим, в  найдется вектор, обозначим его  собственный для оператора А.

Возможны два случая: 1) после конечного числа шагов мы получим подпространство  в котором  на  при всех п.