Абстрактное гильбертово пространство. Интегральные уравнения с симметричным ядром, страница 3

Аналогично определяется сумма любого конечного числа пространств. Сумма  счетного числа пространств  определяется так: элементы пространства Н — это всевозможные последовательности вида

такие, что

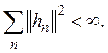
Скалярное произведение (h , g) элементов h и g из Н равно

§ 58. Линейные и билинейные функционалы в гильбертовом пространстве

То обстоятельство, что всякое гильбертово пространство изоморфно пространству L₂, позволяет перенести на абстрактно определенное гильбертово пространство ряд фактов, установленных в гл. III для l₂.

Так как в l₂всякий линейный функционал имеет вид

где а – элемент из l₂, то

любой линейный функционал F(h) в Н можно представить в виде

                                                             (1)

где g зависит только от F.

Отсюда вытекает, что определение слабой сходимости, введенное нами в гл. III для произвольного линейного пространства, применительно к пространству Н может быть сформулировано следующим образом.

Последовательность элементов  пространства Н сходится слабо к  если

1) нормы  ограничены[2];

2) для любого

Любая ортогональная нормированная последовательность

 

в Н слабо сходится к нулю, так как для любого

поскольку

При этом, конечно, по норме такая последовательность ни к какому пределу не сходится.

Применив, в частности, сделанное замечание к тому случаю, когда Н есть пространство функций с интегрируемым квадратом на отрезке [а, b] действительной прямой с обычной лебеговой мерой получим следующий интересный факт. Пусть

– некоторая ортогональная нормированная система функций в этом пространстве, и пусть

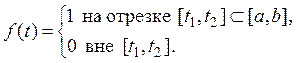
Тогда

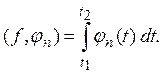
Таким образом, для любой ортогональной нормированной системы функций  и любых t₁ и t₂ из [а, b]

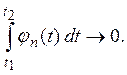
Если  ограничены в совокупности, то при учете условия

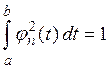
из этого видно, что  с большим номером п неизбежно много раз меняет знак (что и наблюдается, например, в случае тригонометрической системы).

В гл. III мы наряду с понятием слабой сходимости элементов линейного нормированного пространства ввели понятия слабой сходимости последовательности функционалов. Поскольку гильбертово пространство совпадает со своим сопряженным, для него эти два понятия тождественны, поэтому теорема 1 § 28 ч. I для гильбертова пространства Н дает следующий результат:

единичная сфера в Н слабо компактна, т. е. из всякой последовательности элементов  для которых  можно выделить слабо сходящуюся подпоследовательность.

В дальнейшем нам понадобится еще следующая

Теорема 1. Если  слабо сходится к в H, то

Доказательство. Какова бы ни была полная ортогональная нормированная система  в Н, имеем:

и

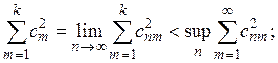
следовательно,

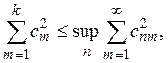
что и доказывает теорему.

Пусть B(f, g) — числовая функция пары векторов из H, удовлетворяющая следующему условию: B(f, g) при фиксированном g есть линейный функционал от f, а при фиксированном f — линейный функционал от g. B(f, g) называется билинейным функционалом. Билинейный функционал B(f, g) называется симметричным, если

Из теоремы об общем виде линейного функционала в H следует, что всякий билинейный функционал в H может быть записан в виде

где  зависит от f. Легко видеть, что соответствие

представляет собой непрерывный линейный оператор в Н;обозначим его А. Таким образом:

                                                    (2)

Аналогично может быть получена и другая запись:

где А* — другой линейный оператор, называемый сопряженным[3] к А. Если функционал  симметричен, то

т.е.

                                                             (3)

Линейный оператор, удовлетворяющий условию (3), называется самосопряженным.

Формула (2) устанавливает взаимно однозначное соответствие между билинейными функционалами и непрерывными линейными операторами в Н. При этом симметричные билинейные функционалы отвечают самосопряженным операторам и обратно.

Положив в симметричном билинейном функционале f = g, мы получим так называемый квадратичный функционал: