Абстрактное гильбертово пространство. Интегральные уравнения с симметричным ядром, страница 2

– счетное всюду плотное множество в R. Пусть, далее,

a  таково, что

Для любого  найдется такое п, что

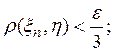
и, следовательно,

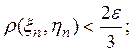
тогда  т. е. счетное множество

всюду плотно в R'.

Существование в пространстве Гильберта скалярного произведения и понятие ортогональности позволяет существенно дополнить результаты, изложенные в первой части курса по поводу замкнутых линейных подпространств произвольных банаховых пространств.

Применив процесс ортогонализации к какой-либо счетной всюду плотной последовательности элементов произвольного подпространства пространства Гильберта, получаем:

Теорема 1. В каждом подпространстве М пространства Н содержится ортогональная система  линейное замыкание которой совпадает с М:

Пусть М – подпространство гильбертова пространства Н. Обозначим

множество элементов  которые ортогональны ко всем  и докажем, что М' тоже есть подпространство пространства Н. Линейность М' очевидна, так как из  вытекает  Для доказательства замкнутости допустим, что  принадлежат М' и сходятся к g. Тогда для любого

и поэтому g тоже входит в М'.

М' называется ортогональным дополнением подпространства М.

Из теоремы 1 легко следует

Теорема 2. Если М — замкнутое линейное подпространство пространства Н, то любой элемент  единственным образом представляется в виде  где

Доказательство. Докажем сначала существование такого разложения. Для этого найдем в М полную ортогональную нормированную систему  (так что ) и положим

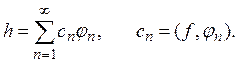
Так как (по неравенству Бесселя) ряд из  сходится, то элемент h существует и входит в М. Положим

Очевидно, что для всех п

и, поскольку любой элемент из М можно представить в виде

то для  имеем:

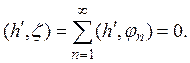
Допустим теперь, что кроме построенного нами разложения  существует еще другое разложение:

Тогда при всех п

откуда вытекает, что

Из теоремы 2 вытекает

Следствие 1. Ортогональное дополнение к ортогональному дополнению замкнутого линейного подпространства М совпадает с самим М.

Таким образом, можно говорить о взаимно дополнительных подпространствах пространства Н. Если М и М' – два такие дополняющие друг друга замкнутые линейные подпространства и  – полные соответственно в М и М' ортогональные системы, то соединение систем  и  дает полную ортогональную систему во всем пространстве Н. Поэтому имеет место

Следствие 2. Каждая ортогональная нормированная система  может быть расширена до системы, полной в Н.

Если система  конечна, то число входящих в нее функций есть размерность пространства М и одновременно индекс пространства М'. Таким образом, получаем

Следствие 3. Ортогональное дополнение к пространству конечной размерности п имеет индекс п, и наоборот.

Если каждый вектор  представлен в виде  (M' – ортогональное дополнение М), то говорят, что Н есть прямая сумма взаимно ортогональных подпространств М и М", и пишут:

Ясно, что понятие прямой суммы может быть непосредственно обобщено на любое конечное или даже счетное число подпространств: именно, говорят, что Н есть прямая сумма своих подпространств

если:

1) подпространства  попарно ортогональны, т. е. любой вектор из  ортогонален любому вектору из  при

2) Каждый элемент  может быть представлен в виде

                                 (1)

причем, если число подпространств  бесконечно, то  – сходящийся ряд. Легко проверить, что такое представление для любого f возможно только одно и что

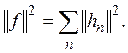
Наряду с прямой суммой подпространств можно говорить о прямой сумме конечного или счетного числа произвольных гильбертовых пространств. Именно, если Н₁ и Н₂ – два гильбертовых пространства, то их прямая сумма Н определяется следующим образом: элементы пространства Н – это всевозможные пары  где  скалярное произведение двух таких пар равно:

В пространстве Н содержатся, очевидно, взаимно ортогональные подпространства, состоящие из пар вида  и  соответственно; первое из них можно естественным образом отождествить с пространством Н₁ а второе – с пространством Н₂.