Абстрактное гильбертово пространство. Интегральные уравнения с симметричным ядром, страница 5

В первом случае из леммы 2 вытекает, что М'_п переводится оператором А в нуль, т.е. целиком состоит из собственных векторов, отвечающих  Система построенных векторов  состоит из конечного числа элементов.

Во втором случае получаем последовательность  собственных векторов, для каждого из которых  Покажем, что  Последовательность  (как и всякая ортогональная нормированная последовательность) слабо сходится к нулю, поэтому элементы  должны сходиться к нулю по норме, откуда

Пусть

Если  то

т.е.

откуда в силу леммы 2 (при max ), примененной к М', получаем  т. е. подпространство М' переводится оператором А в нуль.

Из построения системы  ясно, что всякий вектор можно представить в виде

откуда вытекает, что

§ 60. Линейные уравнения с вполне непрерывными операторами

Рассмотрим уравнение

                                                      (1)

где А – вполне непрерывный самосопряженный оператор, элемент  задан, а  ищется.

Пусть

– собственные векторы оператора А, отвечающие отличным от нуля собственным значениям. Тогда  можно записать в виде

                                                     (2)

где  Будем искать решение уравнения (1) в виде

                                                     (3)

где  Подставив (2) и (3) в (1), получаем:

Это равенство удовлетворяется в том и только том случае, если

т. е. если

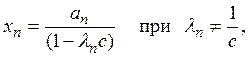                                            (4)

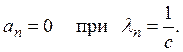
Последнее равенство дает необходимое и достаточное условие разрешимости уравнения (1), а (4) определяет решение. Значения х_п, отвечающие тем п, для которых  остаются произвольными.

§ 61. Интегральные уравнения с симметричным ядром

Изложенные в предыдущем параграфе результаты могут быть применены к интегральным уравнениям с симметричным ядром, т. е. к уравнениям вида

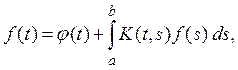                                                (1)

где K(t , s) удовлетворяет условиям

1)

2)

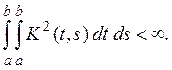
Применение результатов §60 к уравнениям вида (1) основывается на следующей теореме.

Теорема. Пусть R – некоторое пространство с мерой  на нем. Если функция  определенная на  удовлетворяет условиям:

                                                           (2)

и

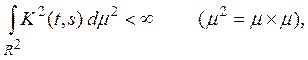                                          (3)

тo оператор

определяемый в пространстве  формулой

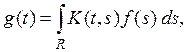
вполне непрерывен и самосопряжен.

Доказательство. Обозначим пространство  просто L₂. Пусть  – полная ортогональная нормированная система в L₂. Совокупность всевозможных произведений  представляет собой полную систему функций в R², и

причем

(в силу (2)), и

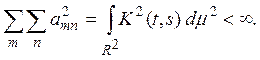
Положим

тогда

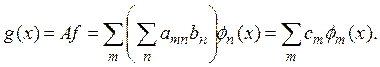
При этом

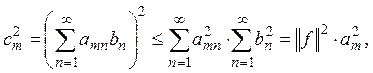
где

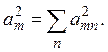
Так как ряд

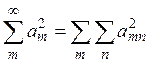
сходится, то можно для любого  найти такое  что

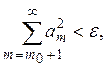
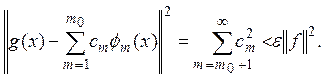                                    (4)

Пусть теперь  сходится слабо к f. Тогда соответствующие  при каждом т будут сходиться к  поэтому сумма

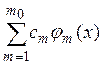
при любом фиксированном  будет сходиться в среднем к сумме

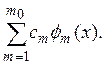
В силу же неравенства (4) и ограниченности норм  отсюда вытекает, что  (где  )будет сходиться в среднем к  что и доказывает полную непрерывность оператора А. Далее, из условия (1) и теоремы Фубини следует, что

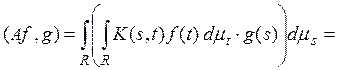
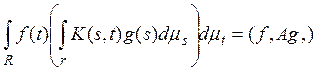       т. е. оператор А – самосопряженный. Теорема доказана. Таким образом, решение интегрального уравнения с ядром, удовлетворяющим условиям (2) и (3), сводится к нахождению собственных функций и собственных значений соответствующего интегрального оператора. Практическое решение этой последней задачи требует обычно привлечения тех или иных приближенных методов, изложение которых выходит за рамки данной книги.