В предыдущей главе мы рассмотрели основные свойства измеримых функций, являющихся весьма широким обобщением непрерывных функций. Для измеримых функций известное из анализа классическое определение интеграла, называемое обычно интегралом Римана, вообще говоря, неприменимо. Например, хорошо известная функция Дирихле, равная нулю в иррациональных точках и единице в рациональных, очевидно, измерима, но не интегрируема в смысле Римана. Таким образом, это понятие интеграла оказывается мало пригодным применительно к измеримым функциям.
Причина этого совершенно ясна. Предположим, для
простоты, что речь идет о функциях на отрезке. Вводя понятие интеграла Римана,
мы разбиваем отрезок, на котором задана некоторая функция f(x), на
маленькие отрезки и, взяв в каждой из этих частей произвольную точку ![]() , составляем сумму
, составляем сумму
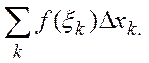
По существу, мы заменяем здесь значение функции
f(x) в каждой из точек
отрезка ![]() ее значением в некоторой произвольно выбранной точке
ее значением в некоторой произвольно выбранной точке ![]() этого интервала. Но это естественно делать
только тогда, когда значения функции f(x) в близких точках близки между собой, т. е. когда f(x) непрерывна или когда множество ее точек разрыва «не слишком
велико»[1].
этого интервала. Но это естественно делать
только тогда, когда значения функции f(x) в близких точках близки между собой, т. е. когда f(x) непрерывна или когда множество ее точек разрыва «не слишком
велико»[1].
Основная идея интеграла Лебега состоит в том, что, в отличие от интеграла Римана, точки х группируются не по признаку их близости на оси х, а по признаку близости значений функции в этих точках. Это сразу дает возможность распространить понятие интеграла на весьма широкий класс функций.
Кроме того, интеграл Лебега определяется совершенно одинаково для функций, заданных на любых пространствах с мерой, в то время как интеграл Римана вводится сначала для функций одного переменного, а затем уже с соответствующими изменениями переносится на случай нескольких переменных.
Всюду, где не оговорено противное, будет
рассматриваться некоторая ![]() -аддитивная мера
-аддитивная мера ![]() , определенная на борелевой алгебре
множеств с единицей X. Все рассматриваемые
множества
, определенная на борелевой алгебре
множеств с единицей X. Все рассматриваемые
множества ![]() будут предполагаться
будут предполагаться ![]() - измеримыми, а функции f(x) — определенными для
- измеримыми, а функции f(x) — определенными для ![]() и
и ![]() - измеримыми.
- измеримыми.
Мы введем понятие интеграла Лебега сначала для функций, названных нами в предыдущей главе простыми, т. е. для измеримых функций, принимающих конечное или счетное число значений.
Пусть f(x) — некоторая простая функция, принимающая значения
![]()
Естественно определить интеграл от функций f(х) по множеству А равенством:
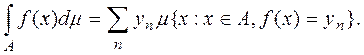 (1)
(1)
Таким образом, мы приходим к следующему определению.
Определение. Простая функция f(x) называется интегрируемой (по мере ![]() )
на множестве А, если ряд (1) абсолютно сходится. Если f(x) интегрируема,
то сумма ряда (1) называется интегралом от (x) по множеству А.
)
на множестве А, если ряд (1) абсолютно сходится. Если f(x) интегрируема,
то сумма ряда (1) называется интегралом от (x) по множеству А.
В этом определении
предполагается, что все ![]() различны. Можно,
однако, представить значение интеграла от простой функции, в виде суммы
произведений вида
различны. Можно,
однако, представить значение интеграла от простой функции, в виде суммы
произведений вида ![]() и не предполагая, что все
и не предполагая, что все
![]() различны. Это позволяет сделать следующая
различны. Это позволяет сделать следующая
Лемма. Пусть ![]() при
при ![]() , и пусть на каждом множестве
, и пусть на каждом множестве ![]() функция f(x)
принимает только одно значение
функция f(x)
принимает только одно значение ![]() тогда
тогда
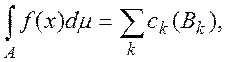 (2)
(2)
причем функция f(x) интегрируема на А в том и только том случае, когда ряд (2) абсолютно сходится.
Доказательство. Легко видеть, что каждое множество
![]()
является соединением тех ![]() , для
которых
, для
которых ![]() . Поэтому
. Поэтому
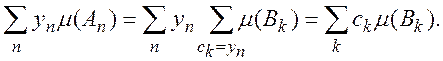
Так как мера неотрицательна, то
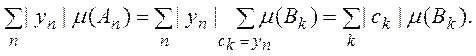
т.е. ![]() и
и ![]() абсолютно сходятся или расходятся
одновременно.
абсолютно сходятся или расходятся
одновременно.
Установим некоторые свойства интеграла Лебега от простых функций:
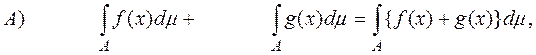
причем из существования интегралов в левой части следует существование интеграла в правой части.
Для доказательства предположим, что f(x) принимает значения ![]() на
множествах
на
множествах ![]() а g(х) — значения
а g(х) — значения ![]() на множествах
на множествах ![]() так что
так что
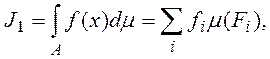 (3)
(3)
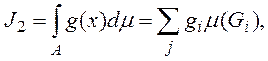 (4)
(4)
Тогда, в силу леммы,
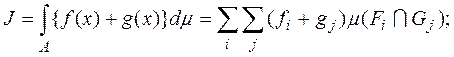 (5)
(5)
но
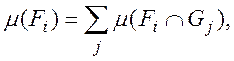
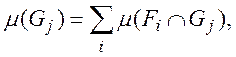
так что из абсолютной сходимости рядов (3) и (4) следует и абсолютная сходимость ряда (5); при этом
![]()
Б) Для любого постоянного ![]() ,
,
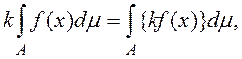
причем из существования интеграла в левой части следует существование интеграла в правой части. (Проверяется непосредственно.)
В) Ограниченная на множестве А простая
функция f(x) интегрируема на A, причем, если ![]() на А, то
на А, то
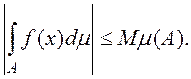
(Проверяется непосредственно.)
Определение. Будем называть функцию f(x) интегрируемой на множестве А, если
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.