Определение и основные свойства измеримых функций

Глава VI

Измеримые функции

§ 40. Определение и основные свойства измеримых функций

Пусть X и Y — два произвольных множества и пусть в них выделены две системы подмножеств и соответственно. Абстрактная функция с областью определения X, принимающая значения из Y, называется (,)-измеримой, если из вытекает, что .

Например, если и за X и за Y взять числовую прямую D¹ (т. е. рассматривать действительные функции действительного переменного), а за и взять систему всех открытых (или всех замкнутых) подмножеств из D¹, то сформулированное определение измеримости сведется к определению непрерывности (§ 12). Взяв за  и  систему всех борелевских множеств, мы придем к так называемым B-измеримым (или измеримым по Борелю) функциям.

В дальнейшем мы будем интересоваться понятием измеримости главным образом с точки зрения теории интегрирования. В этом плане основное значение имеет понятие  - измеримости действительных функций, определенных на некотором множестве X, причем за  принимается система всех - измеримых подмножеств множества X, а за  — совокупность всех В-множеств на прямой. Для простоты мы будем считать, что X есть единица области определения , меры . Так как, в силу результатов § 38, всякая - аддитивная мера может быть продолжена на некоторую борелевскую алгебру, естественно с самого начала считать, что S, есть В-алгебра. Таким образом, для действительных функций мы сформулируем определение измеримости так:

Определение 1. Действительная функция f(x), определенная на множестве X, называется - измеримой, если для любого борелевского множества А числовой прямой

Обозначим через {х : Q} множество тех , для которых выполнено условие Q. Справедлива следующая

Теорема 1. Для того чтобы функция f(x) была измерима, необходимо и достаточно, чтобы при любом действительном с множество  было  измеримо (т. е. принадлежало ).

Доказательство. Необходимость условия ясна, так как полупрямая  есть борелевское множество. Для доказательства достаточности заметим прежде всего, что борелевское замыкание системы  всех полупрямых  совпадает с системой всех борелевских множеств числовой прямой. По условию, . Но тогда

Но , так как, по условию,  есть B-алгебра. Теорема доказана.

Теорема 2. Предел сходящейся при каждом  последовательности  измеримых функций - измерим.

Доказательство. Пусть  тогда

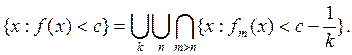                                    (1)

Действительно, если , то существует такое , что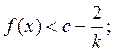

далее, при этом можно найти столь большое п, что при выполнено неравенство

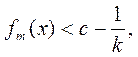
а это и означает, что х войдет в правую часть (1).

Обратно, если х принадлежит правой части равенства (1), то существует такое , что при всех достаточно больших т

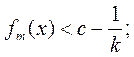
но тогда , т. е. х входит, в левую часть равенства (1).

Если функции измеримы, то множества

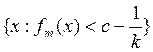
принадлежат . Так как  есть борелевская алгебра, то, в силу (1), множества

тоже принадлежат , что и доказывает измеримость f(x).

Для дальнейшего изучения измеримых функций удобно каждую m них представлять как предел последовательности так называемых простых функций.

Определение 2. Функция f(x) называется простой, если она - измерима и принимает не более чем счетное число значений.

Ясно, что понятие простой функции зависит от выбора меры .

Структура простых функций характеризуется следующей теоремой:

Теорема 3. Функция f(x), принимающая не более чем счетное число различных значений

- измерима в том и только том случае, если все множества

 - измеримы.

Доказательство. Необходимость условия ясна, так как каждое  есть прообраз одноточечного множества а всякое одноточечное множество является борелевским. Достаточность следует из того, что в условиях теоремы прообраз любого множества есть соединение  не более чем счетного числа измеримых множеств , т.е. измерим.

Дальнейшее использование простых функций будет основано на следующей теореме.

Теорема 4. Для  - измеримости функции f(x) необходимо и достаточно, чтобы она могла быть представлена в виде предела равномерно сходящейся последовательности простых функций.

Доказательство. Достаточность ясна из теоремы 2. Для доказательства необходимости рассмотрим произвольную измеримую функцию f(x)и положим 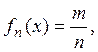когда 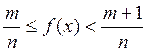(здесь т — целые, а п — целые положительные). Ясно, что функции — простые; при  они равномерно сходятся к f(x), так как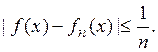

Теорема 5. Сумма двух  - измеримых функций - измерима.

Доказательство. Докажем сначала это утверждение для простых функций. Если f(x) и g(х) — две простые функции, принимающие соответственно значения

и

то их сумма h(x) = f(x) + g(x) может принимать только значения  причем