Линейные нормированные пространства

Глава III

Линейные нормированные пространства

§ 21. Определение и примеры линейных нормированных пространств

Определение 1. Совокупность R элементов  называется линейным пространством, если выполнены следующие условия:

I. Для любых двух элементов  однозначно определен третий элемент  называемый их суммой, причем

1)

2)

3) существует элемент 0 такой, что  для всех

4) Для каждого  существует такой элемент  что

II. Для любого числа  и элемента  определен элемент  (произведение элемента х на число ), причем:

1)

2)

III. Операции сложения и умножения связаны следующим образом:

1)

2)

В зависимости от того, какой запас чисел (все комплексные или только действительные) допускается, различают комплексные и действительные линейные пространства. Всюду, где не оговорено противное, мы будем рассматривать действительные линейные пространства.

В линейном пространстве, помимо операций сложения и умножения на числа, вводится еще обычно тем или иным способом операция предельного перехода. Наиболее удобно это сделать, введя в линейном пространстве норму.

Линейное пространство R называется нормированным, если каждому элементу  поставлено в соответствие неотрицательное число  норма  причем:

1) тогда и только тогда, когда

2)

3)

Легко видеть, что всякое нормированное пространство является в то же время метрическим пространством; достаточно положить  Справедливость аксиом метрического пространства непосредственно вытекает из свойств 1-3 нормы.

Полное нормированное пространство называется пространством типа Банаха, или, короче, В-пространством.

Примеры нормированных пространств. 1. Прямая линия с обычными арифметическими операциями представляет собой простейший пример нормированного пространства. Норма в этом случае есть просто абсолютная величина действительного числа.

2. n-мерное евклидово пространство, т.е. пространство, состоящее из систем п действительных чисел:  в котором норма (т. е. длина) вектора определяется как корень квадратный из его скалярного квадрата

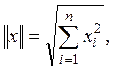
есть также нормированное линейное пространство.

В n-мерном линейном пространстве норму вектора

можно также определить формулой

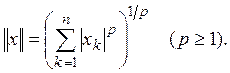
Полагая норму вектора  равной  мы опять-таки получаем нормированное пространство.

3. Пространство  непрерывных функций с обычными для функций операциями сложения и умножения на числа, в котором

является линейным нормированным пространством.

4. Пусть  опять-таки состоит из всех непрерывных функций на отрезке [а, b], а норма вводится формулой

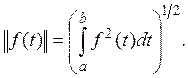
Все аксиомы нормы здесь выполнены.

5. Пространство  является линейным нормированным пространством, если положить, что сумма двух элементов

из  есть

а

и

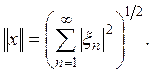
6. Пространство с состоит из последовательностей

действительных чисел, удовлетворяющих условию

Сложение и умножение определяются как и в примере 5, а норма полагается равной

7. Пространство т ограниченных последовательностей с теми же самыми определениями суммы, произведения и нормы, что и в предыдущем примере.

Аксиомы линейного пространства в каждом из этих примеров проверяются без труда. Тот факт, что в примерах 1-5 выполняются аксиомы 1-3 для нормы, доказывается в точности так же, как и справедливость аксиом метрического пространства в соответствующих примерах § 8 гл. II.

Все перечисленные в примерах пространства, кроме пространства  являются B-пространствами.

Определение 2. Линейным многообразием L в линейном нормированном пространстве R называется всякое множество элементов из R, удовлетворяющих следующему условию: если  то  где  и  — любые числа. Замкнутое линейное многообразие в R называется подпространством пространства R.

Замечание 1. В n-мерном евклидовом пространстве R понятия линейного многообразия и подпространства совпадают, так как всякое линейное многообразие в  автоматически замкнуто. (Докажите это!) Напротив, в бесконечномерном пространстве существуют и незамкнутые линейные многообразия. Например, в  множество L точек вида

                                                   (1)

т. е. таких точек, которые имеют лишь конечное (но любое) число отличных от нуля координат, представляет собой незамкнутое линейное многообразие. Действительно, линейная комбинация точек вида (1) есть точка такого же вида, т. е. L — линейное многообразие. Но L не замкнуто, так как, например, последовательность точек

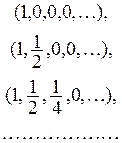
принадлежащих L, сходится к точке

которая L не принадлежит.

Замечание 2. Пусть  — элементы банахова пространства R, а М — совокупность элементов R вида 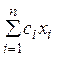 при любом конечном п.

Очевидно, что М есть линейное многообразие в R. Покажем, что [М] есть линейное подпространство. Ввиду замкнутости [М] достаточно доказать, что оно является линейным многообразием.

Пусть  Тогда в любой -окрестности х найдется  а в любой -окрестности у — точка  Составим элемент  и оценим