Линейные нормированные пространства, страница 3

Пусть А — произвольное множество, лежащее в некотором линейном нормированном пространстве. Назовем выпуклым замыканием множества А наименьшее замкнутое выпуклое множество, содержащее А.

Выпуклое замыкание всякого множества может быть, очевидно, получено как пересечение всех замкнутых выпуклых множеств, содержащих данное множество.

Рассмотрим один важный пример выпуклого замыкания.

Пусть  — точки из некоторого линейного нормированного пространства. Мы скажем, что эти п + 1 точка находятся в общем положении, если никакие три из них не лежат на одной прямой, никакие четыре не лежат в одной плоскости и т. д., вообще никакие k + 1 из этих точек не лежат в подпространстве размерности меньше, чем k. Выпуклое замыкание точек  находящихся в общем положении, называется п-мерным симплексом, а сами точки  — его вершинами. Нульмерный симплекс — это одна точка. Одномерный симплекс — отрезок, двумерный — треугольник, трехмерный — тетраэдр.

Если точки  лежат в общем положении, то любые k + 1 из них (k < п) также лежат в общем положении и, следовательно, порождают некоторый k-мерный симплекс, называемый k-мерной гранью данного n-мерного симплекса. Например, тетраэдр с вершинами  имеет четыре двумерные грани, определяемые соответственно тройками вершин  шесть одномерных граней и четыре нульмерных.

Теорема 3. Симплекс с вершинами  есть совокупность всех точек, которые можно представить в виде

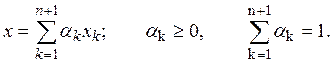                                       (2)

Доказательство. Действительно, легко проверить, что совокупность точек вида (2) представляет собой замкнутое выпуклое множество, содержащее точки  С другой стороны, всякое выпуклое множество, содержащее точки  должно содержать и точки вида (2), следовательно, эти точки образуют наименьшее замкнутое выпуклое множество, содержащее точки

§ 23. Линейные функционалы

Определение 1. Числовую функцию f(x), определенную на некотором линейном нормированном пространстве R, мы будем называть функционалом. Функционал f(x) называется линейным, если

где  — произвольные числа.

Функционал f(x) называется непрерывным в точке  если для любого  найдется такое  что из неравенства

следует, что

В дальнейшем мы будем рассматривать только непрерывные функционалы (в частности, непрерывные линейные функционалы), причем слово «непрерывный» будем для краткости опускать.

Установим некоторые свойства линейных функционалов, почти непосредственно вытекающие из определения.

Теорема 1. Если линейный функционал f(x) непрерывен в какой-либо одной точке  то он непрерывен и всюду на R.

Доказательство. Действительно, пусть линейный функционал f(x) непрерывен в точке  Это равносильно тому, что

Пусть, далее, Тогда

Но  Следовательно, по предположению  Таким образом,

Функционал f(x) называется ограниченным, если существует такое постоянное число N, что

                                                             (1)

для всех

Теорема 2. Для линейных функционалов условия непрерывности и ограниченности эквивалентны.

Доказательство. Предположим, что линейный функционал f(x) не ограничен. Тогда для любого натурального п найдется такой элемент  что  Положим, 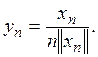 Тогда  т. е.  Но в то же время

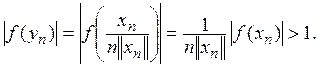
Следовательно, в точке x = 0 функционал f(x) не непрерывен.

Пусть теперь число N, удовлетворяющее условию (1), существует. Тогда для любой последовательности  имеем:

т. е. f(x) непрерывен в точке x = 0, а следовательно, и во всех остальных. Теорема доказана.

Определение 2. Величина

называется нормой линейного функционала f(x).

Примеры линейных функционалов в различных пространствах. 1.

Пусть  — n-мерное евклидово пространство и а — какой-либо фиксированный вектор в нем. Положим для любого  где (х, а) — скалярное произведение векторов x и а. Ясно, что f(x) — линейный функционал. Действительно,

Далее, в силу неравенства Буняковского,

                                                     (2)

Следовательно, функционал f(x) ограничен и потому непрерывен. Из (2) находим

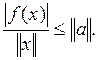
Так как правая часть этого неравенства не зависит от х, то