Линейные нормированные пространства, страница 6

Рассмотрим случай, когда это совпадение имеет место и в бесконечномерном пространстве.

4. Пространство  состоит из последовательностей

таких, что 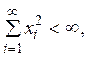 с нормой 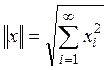 Функционалы в пространстве  все имеют вид

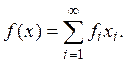
Докажем это утверждение.

Каждому функционалу ставится в соответствие последовательность  его значений на элементах  определяемых так же, как на стр. 84.

Если функционал ограничен, то 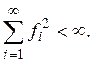 Предположим противное, т. е. предположим, что для всякого Н найдется такое N, что

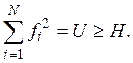
Применив рассматриваемый функционал к элементу

получим

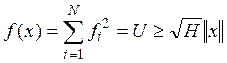
вопреки предположению об ограниченности функционала.

Так как функционал f линейный, то легко находятся его значения на элементах вида  на всех прочих элементах пространства они находятся из соображений непрерывности и всегда

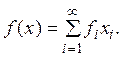
Норма функционала равна 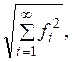 что устанавливается с помощью неравенства Буняковского.

5. Пространство  — пространство последовательностей:

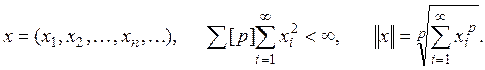
Пространством, сопряженным с  является пространство  где

Доказательство аналогично предыдущим. Используется неравенство Гельдера.

§ 25. Продолжение линейных функционалов

Теорема (Хана-Банаха). Всякий линейный функционал f(x), определенный на линейном подпространстве G линейного нормированного пространства Е, можно продолжить на все пространство с сохранением нормы, т. е. можно построить такой линейный функционал F(x), что

1)

2)

Доказательство. Теорема будет доказана для сепарабельного пространства Е, хотя в действительности она верна и в несепарабельном случае.

Сначала распространим функционал на линейное подпространство  полученное добавлением к G некоторого элемента  Любой элемент этого подпространства однозначно представляется в виде

Если искомый функционал существует, то

или, если положить

Чтобы норма функционала не увеличилась при его продолжении, надо найти такое с, чтобы неравенство

                                                   (1)

выполнялось для всех

Неравенство (1) эквивалентно следующим неравенствам:

или, что то же,

Обозначив через z элемент  получим, что искомое число с должно удовлетворять условию

для всех  Докажем, что такое число с всегда существует. Для этого покажем, что каковы бы ни были элементы  всегда

                                   (2)

Но это непосредственно вытекает из очевидного неравенства

            

Введем обозначения:

Из неравенства (2) следует, что

Возьмем любое с, такое, что  Положим,

на элементах множества  Получим линейный функционал  причем

В сепарабельном пространстве Е имеется счетное всюду плотное множество  Будем строить линейные подпространства

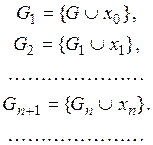
и распространять на них функционал последовательно, т. е. строить функционалы  совпадающие с  на  и имеющие норму, равную  Таким образом, получим функционал F, определенный на множестве, всюду плотном в Е. На остальных точках Е функционал доопределяется по непрерывности: если  то  Неравенство  выполняется, так как

Теорема о продолжении функционала доказана.

Следствие. Пусть  — произвольный, отличный от нуля элемент в R и пусть М — произвольное положительное число. Тогда в R существует такой линейный функционал f(x), что

Действительно, положив

мы получим линейный функционал с нормой, равной М, определенный на одномерном подпространстве элементов вида  а затем, по теореме Хана-Банаха, его можно продолжить на все R без увеличения нормы. Геометрически это означает следующее: в банаховом пространстве через каждую точку  можно провести гиперплоскость, опорную к сфере

§ 26. Второе сопряженное пространство

Так как совокупность  линейных функционалов на некотором линейном нормированном пространстве R сама представляет собой линейное нормированное пространство, то можно говорить о пространстве  линейных функционалов на  т.е. о втором сопряженном к R т.д. Заметим прежде всего, что всякий элемент из R определяет некоторый линейный функционал на  Действительно, пусть

где  — некоторый фиксированный элемент из R, а f пробегает все  Таким образом, каждому  поставлено в соответствие некоторое число  При этом