Линейные нормированные пространства, страница 2

откуда видно, что

Подпространство L = [М] называется подпространствам, порожденным элементами

§ 22. Выпуклые множества в линейных нормированных пространствах

Пусть х и у — две точки в линейном пространстве R. Назовем отрезком, соединяющим точки х и у, совокупность всех точек вида  где

Определение. Множество М в линейном пространстве R называется выпуклым, если, каковы бы ни были две точки х, у, принадлежащие М, соединяющий их отрезок также принадлежит М. Выпуклое множество называется выпуклым телом, если оно содержит хотя бы одну внутреннюю точку, т. е. если оно целиком содержит некоторую сферу.

Примеры. 1. В трехмерном евклидовом пространстве куб, сфера, тетраэдр, полупространство являются выпуклыми телами, а треугольник, плоскость, отрезок — выпуклыми множествами, но не выпуклыми телами.

2. Сфера в линейном нормированном пространстве всегда является выпуклым множеством (и одновременно выпуклым телом). Действительно, рассмотрим, для простоты записи, единичную сферу S:

Пусть  — две какие-либо точки, принадлежащие этой сфере:

Тогда

т.е.

3. Пусть R — совокупность векторов  на плоскости. Введем в R следующие не совпадающие между собой нормы:

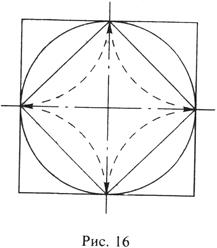Посмотрим, какой будет единичная сфера для каждой из этих норм. В случае  — это круг радиуса 1, в случае  — квадрат с вершинами (1, 1), в случае  — квадрат с вершинами (0, 1); (1, 0); ( – 1, 0); (0, – 1). Если рассмотреть единичную сферу, соответствующую норме  и увеличивать р от 1 до  то эта «сфера» будет непрерывно деформироваться от квадрата, соответствующего  до квадрата, соответствующего . Если бы мы положили

при р > 1, то множество  не было бы выпуклым (например, при  это была бы внутренность астроиды). Это иное выражение того факта, что при р < 1 «норма» (1) не удовлетворяет условию 3 определения нормы.

4. Рассмотрим несколько более сложный пример. Пусть Ф — множество точек

из  удовлетворяющих условию

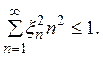
Это выпуклое множество в  не являющееся выпуклым телом. Действительно, если  и где  и  то в силу неравенства Коши-Буняковского (гл. II),

    

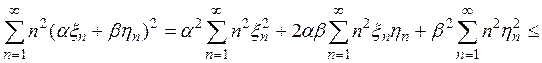
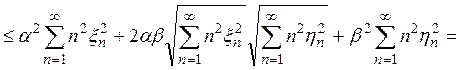
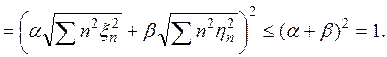
Покажем, что Ф не содержит никакой сферы. Так как Ф симметрично относительно начала координат, то, если бы Ф содержало какую-либо сферу  оно содержало бы и сферу  симметричную с  относительно начала координат. Тогда Ф, будучи выпуклым, содержит все отрезки, соединяющие точки сфер  и  а следовательно, и сферу S того же радиуса, что и  с центром в начале координат. Но если бы Ф содержало некоторую сферу радиуса r с центром в нуле, то на каждом луче, выходящем из нуля, имелся бы отрезок, целиком принадлежащий Ф. Однако на луче, определяемом вектором  нет, очевидно, ни одной точки, кроме нуля, принадлежащей Ф.

Упражнения. 1) Доказать компактность множества Ф. Доказать, что никакое компактное выпуклое множество в  не может быть выпуклым телом.

2) Доказать, что Ф не содержится ни в каком подпространстве, отличном от всего

3) Доказать, что фундаментальный параллелепипед в  (см. пример 3 § 16) является выпуклым множеством, но не выпуклым телом.

Установим простейшие свойства выпуклых множеств.

Теорема 1. Замыкание выпуклого множества есть снова выпуклое множество.

Доказательство. Пусть М — выпуклое множество, [М] — его замыкание и х, у — две произвольные точки из [М]. Пусть, далее,  — произвольное положительное число. В М найдутся такие точки а, b, что  и  Тогда для любых неотрицательных  и  таких, что  точка  принадлежит М, так как М выпукло. Так как  произвольно, то отсюда следует, что  т. е. [М] также выпукло.

Теорема 2. Пересечение любого числа выпуклых множеств есть выпуклое множество.

Доказательство. Пусть  и все  — выпуклые множества. Пусть, далее, х и u— две произвольные точки из М. Эти точки х и у принадлежат всем  Тогда отрезок, соединяющий точки х и у, принадлежит каждому  а следовательно, он принадлежит и М. Таким образом, М действительно выпукло.

Так как пересечение замкнутых множеств всегда замкнуто, то отсюда следует, что

пересечение любого числа замкнутых выпуклых множеств есть замкнутое выпуклое множество.