Определение
1. Обобщенной функцией (на прямой ![]() ) называется всякий линейный функционал
) называется всякий линейный функционал ![]() определенный на пространстве D. Таким образом,
определенный на пространстве D. Таким образом, ![]() удовлетворяет следующим
условиям:
удовлетворяет следующим
условиям:
1. ![]()
2. Если ![]() (в указанном выше смысле), то
(в указанном выше смысле), то ![]()
Рассмотрим некоторые примеры.
1. Пусть f(t) — произвольная
непрерывная функция от t. Тогда, так как каждая
функция ![]() равна нулю вне некоторого конечного интервала,
интеграл
равна нулю вне некоторого конечного интервала,
интеграл
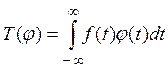 (1)
(1)
существует для всех ![]() Выражение
(1) представляет собой линейный функционал на D (читателю предоставляется проверить, что условия 1 и 2 определения
1 действительно выполнены), т. е. некоторую обобщенную функцию. Таким образом,
всякая «обычная» непрерывная функция является в то же время и обобщенной
функцией.
Выражение
(1) представляет собой линейный функционал на D (читателю предоставляется проверить, что условия 1 и 2 определения
1 действительно выполнены), т. е. некоторую обобщенную функцию. Таким образом,
всякая «обычная» непрерывная функция является в то же время и обобщенной
функцией.
При этом две различные
непрерывные функции будут определять на D различные функционалы, т.е. будут представлять собой
различные обобщенные функции. Достаточно, очевидно, показать, что всякая
отличная от тождественного нуля непрерывная функция f(t) определяет не равный нулю линейный функционал, т. е.
показать, что найдется такая функция ![]() для которой
для которой
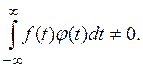
Так как ![]() то найдется интервал
то найдется интервал ![]() на котором f(t) отлична от нуля и, следовательно, сохраняет знак (например,
положительна). Рассмотрим функцию
на котором f(t) отлична от нуля и, следовательно, сохраняет знак (например,
положительна). Рассмотрим функцию
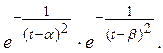
Эта функция на интервале ![]() положительна, а в его концах обращается в
нуль вместе со своими производными всех порядков. Следовательно, функция
положительна, а в его концах обращается в
нуль вместе со своими производными всех порядков. Следовательно, функция ![]() равная
равная ![]() на интервале
на интервале ![]() и равная нулю
вне этого интервала, имеет непрерывные производные всех порядков, т. е. принадлежит
D.
Далее,
и равная нулю
вне этого интервала, имеет непрерывные производные всех порядков, т. е. принадлежит
D.
Далее,
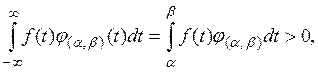
так как подынтегральная функция положительна.
2. Положим теперь
![]() (2)
(2)
Формула (2) определяет
некоторый линейный функционал на D, т.е. некоторую
обобщенную функцию. Это не что иное, как уже упоминавшаяся нами ![]() -функция[5].
-функция[5].
3. Положим,
![]()
Эта обобщенная функция называется производной
от ![]() -функции и обозначается
-функции и обозначается ![]() (Общее определение производной от
обобщенной функции будет дано ниже.)
(Общее определение производной от
обобщенной функции будет дано ниже.)
Иногда обобщенную функцию
удобно обозначать, как и обычную функцию, символом ![]() говоря,
что линейный функционал Т «определяется» некоторый обобщенной функцией f(t). Само значение
говоря,
что линейный функционал Т «определяется» некоторый обобщенной функцией f(t). Само значение ![]() линейного функционала Т
для каждой функции
линейного функционала Т
для каждой функции ![]() при этом удобно записывать в
виде «скалярного произведения» (
при этом удобно записывать в
виде «скалярного произведения» (![]() ). Если f(t) — «настоящая» функция, то
). Если f(t) — «настоящая» функция, то
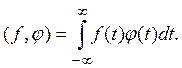
Часто, особенно в физических работах, такую интегральную запись используют и для обобщенных функций, например, пишут:
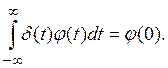
Однако необходимо при этом отчетливо представлять себе, что такой интеграл представляет собой лишь условную запись значения соответствующего функционала и не имеет никакого другого смысла.
Введем теперь понятие предела последовательности обобщенных функций.
Определение
2. Последовательность ![]() называется сходящейся к обобщенной функции
Т, если
называется сходящейся к обобщенной функции
Т, если ![]() равномерно на всяком
«ограниченном» множестве из D. При этом множество
равномерно на всяком
«ограниченном» множестве из D. При этом множество ![]() называется ограниченным, если: 1)
существует такой конечный интервал, вне которого все
называется ограниченным, если: 1)
существует такой конечный интервал, вне которого все ![]() из
этого множества равны нулю, и 2) можно подобрать такие постоянные
из
этого множества равны нулю, и 2) можно подобрать такие постоянные ![]() что
что
![]()
для всех ![]()
Легко проверить, что в
смысле этого определения ![]() -функция является
пределом, например, такой последовательности «настоящих» функций:
-функция является
пределом, например, такой последовательности «настоящих» функций:
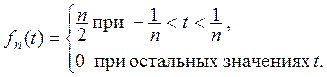
Точно так же легко
построить последовательность настоящих функций, сходящихся в указанном смысле к
обобщенной функции ![]() Вообще
можно доказать, что всякая обобщенная функция есть предел некоторой
последовательности линейных функционалов, определяемых «настоящими» функциями.
Вообще
можно доказать, что всякая обобщенная функция есть предел некоторой
последовательности линейных функционалов, определяемых «настоящими» функциями.
Сформулируем теперь определение производной от обобщенной функции.
Рассмотрим сперва линейный функционал Т, определяемый некоторой дифференцируемой функцией:
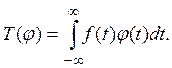
Его производной ![]() естественно
назвать функционал, определяемый формулой
естественно
назвать функционал, определяемый формулой
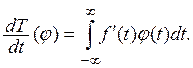
Пользуясь формулой
интегрирования по частям и учитывая, что всякая функция ![]() дифференцируема
и равна нулю вне некоторого конечного интервала, последнее выражение можно
переписать в виде
дифференцируема
и равна нулю вне некоторого конечного интервала, последнее выражение можно
переписать в виде
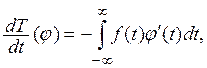
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.