Линейные нормированные пространства, страница 4

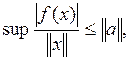
т.е.  Но, положив x = a, получим:

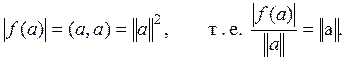
Поэтому

2. Интеграл

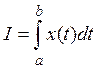
(x(t) — непрерывная функция на [а, b]) представляет собой линейный функционал в пространстве  Его норма равна b — а. Действительно,

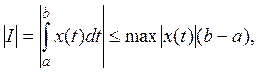
причем при  выполняется равенство.

3. Рассмотрим более общий пример. Пусть  — некоторая фиксированная непрерывная функция на [а, b]. Положим, для любой функции

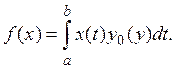
Это выражение представляет собой линейный функционал на  так как

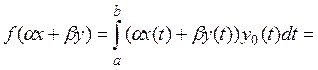
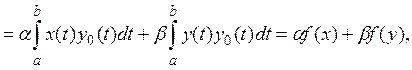
Этот функционал ограничен. Действительно,

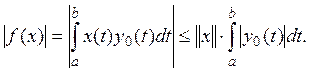
Таким образом, функционал f(x) линеен и ограничен, а следовательно, и непрерывен. Можно показать, что его норма в точности равна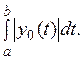

4. Рассмотрим в том же самом пространстве  линейный функционал другого типа, а именно, положим,

т.е. значение функционала  для функции x(t) равно значению этой функции в фиксированной точке  Этот функционал часто приходится рассматривать, например, в квантовой механике, где его обычно пишут в виде

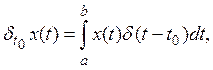
понимая под  «функцию», которая равна нулю всюду, кроме точки  и интеграл от которой равен единице (-функция Дирака), -функцию можно представить себе как предел, в некотором смысле, последовательности функций  каждая из которых обращается в нуль вне некоторой -окрестности  при  точки t = 0 и интеграл от которой равен 1.

5. В пространстве  можно определить линейный функционал так же, как и в  выбрав в  некоторый фиксированный элемент  и положив

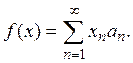                                                          (3)

Ряд (3) сходится для любого  и

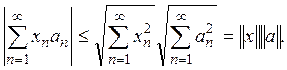                                          (4)

При  неравенство (4) превращается в тождество

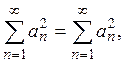
следовательно,

Геометрический смысл линейного функционала. Пусть f(x) — некоторый линейный функционал в пространстве R, причем f(x) не равен нулю тождественно. Совокупность  тех элементов из R, которые удовлетворяют условию

представляет собой подпространство. Действительно, если  то

т. е.  Далее, если  и  то в силу непрерывности функционала f

Определение 3. Говорят, что подпространство L банахова пространства R имеет индекс s, если в пространстве R можно найти s линейно независимых элементов  не принадлежащих L, таких, что всякий элемент  представляется в виде

причем меньшего числа элементов  обладающих указанными свойствами, найти нельзя.

В случае конечномерного пространства R индекс дополняет размерность подпространства L до размерности всего пространства.

Теорема 3. Пусть дан функционал  Подпространство  имеет индекс, равный единице, т. е. любой элемент  представляется в виде

причем  — фиксированный элемент, не принадлежащий

Доказательство. Так как  то  Положив

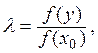
a

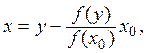
получим, что  причем

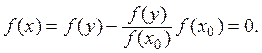f

Если элемент  фиксирован, то элемент у представляется в виде (5) единственным образом, что легко доказывается от противного. Действительно, пусть

тогда

Если  то очевидно, что  Если же то  что противоречит условию

Подпространство  определяет функционал f(x), обращающийся на нем в нуль, с точностью до множителя.

Рассмотрим теперь совокупность  элементов из R, удовлетворяющих условию  можно представить в виде

где  — некоторый фиксированный элемент, такой, что  и  — совокупность элементов, удовлетворяющих условию  По аналогии с конечномерным случаем  естественно назвать гиперплоскостью в пространстве R. Легко проверить, что гиперплоскости  и  совпадают тогда и только тогда, когда функционалы f и  совпадают. Таким образом, можно установить взаимно однозначное соответствие между всеми функционалами, определенными на R, и всеми гиперплоскостями в R, не проходящими через начало координат.

Найдем расстояние от гиперплоскости  до начала координат.

Оно равно

Для всех x, таких, что  имеем

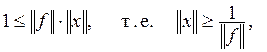
поэтому 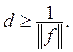 Далее, так как для любого  найдется такой элемент х, удовлетворяющий условию  что  то

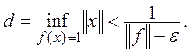
Следовательно,

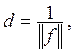
т.е. норма линейного функционала f(x) равна обратной величине расстояния гиперплоскости f(x) = 1 от начала координат.

§ 24. Сопряженное пространство

Для линейных функционалов можно определить операции сложения и умножения на числа. Пусть  и  — два линейных функционала на некотором линейном нормированном пространстве R. Их суммой называется такой линейный функционал  что