Доказательство. Выберем в R счетное всюду плотное множество ![]() Если
Если ![]() ограниченная (по норме) последовательность
линейных функционалов на R, то
ограниченная (по норме) последовательность
линейных функционалов на R, то
![]()
ограниченная числовая последовательность.
Поэтому из ![]() можно выбрать подпоследовательность
можно выбрать подпоследовательность
![]()
так, чтобы числовая последовательность
![]()
сходилась. Далее, из подпоследовательности ![]() подпоследовательность
подпоследовательность
![]()
так, чтобы
![]()
сходилась, и т. д. Таким образом, мы получим систему последовательностей
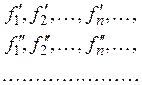
из которых каждая следующая есть подпоследовательность предыдущей. Взяв затем «диагональную» подпоследовательность
![]()
мы получим последовательность линейных функционалов такую, что
![]()
сходится для всех п. Но тогда ![]() сходится и для любого
сходится и для любого ![]() Теорема доказана.
Теорема доказана.
Последняя теорема
подсказывает следующий вопрос. Нельзя ли в пространстве ![]() сопряженном
к сепарабельному, ввести метрику так, чтобы ограниченные подмножества
пространства
сопряженном
к сепарабельному, ввести метрику так, чтобы ограниченные подмножества
пространства ![]() в этой новой метрике были компактны. Иначе
говоря, нельзя ли в
в этой новой метрике были компактны. Иначе
говоря, нельзя ли в ![]() ввести метрику так, чтобы в
каждом ограниченном подмножестве пространства
ввести метрику так, чтобы в
каждом ограниченном подмножестве пространства ![]() сходимость
в смысле этой метрики в
сходимость
в смысле этой метрики в ![]() совпадала со слабой
сходимостью элементов из
совпадала со слабой
сходимостью элементов из ![]() как линейных
функционалов. Такую метрику в
как линейных
функционалов. Такую метрику в ![]() действительно можно
ввести.
действительно можно
ввести.
Пусть ![]() счетное всюду плотное множество в R. Положим, для любых двух
счетное всюду плотное множество в R. Положим, для любых двух ![]()
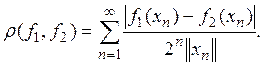 (2)
(2)
Этот ряд сходится, так как его n-й член не
превосходит 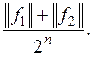 Величина (2) обладает всеми свойствами расстояния.
Действительно, первые две аксиомы очевидны; проверим аксиому треугольника.
Величина (2) обладает всеми свойствами расстояния.
Действительно, первые две аксиомы очевидны; проверим аксиому треугольника.
Так как
![]()
![]()
то
![]()
Непосредственная проверка
показывает, что для ограниченных последовательностей из ![]() сходимость
в смысле этой метрики действительно эквивалентна слабой сходимости в
сходимость
в смысле этой метрики действительно эквивалентна слабой сходимости в ![]()
Теперь теорема 1 может быть сформулирована следующим образом:
Теорема 1'. В пространстве R, сопряженном к сепарабельному, с метрикой (2) всякое ограниченное подмножество компактно.
1. Определение линейного оператора. Ограниченность и непрерывность
Имеются два банаховых
пространства R и R', элементы которых
обозначаются соответственно через х и у. Пусть дан закон, по
которому каждому х из некоторого множества ![]() ставится
в соответствие некоторый элемент у из пространства R'. Тогда говорят, что на
множестве X определен оператор
у = Ах с областью значений из R'.
ставится
в соответствие некоторый элемент у из пространства R'. Тогда говорят, что на
множестве X определен оператор
у = Ах с областью значений из R'.
Определение
1. Оператор А называется линейным,
если для любых двух элементов ![]() и любых действительных
чисел
и любых действительных
чисел ![]() выполняется равенство
выполняется равенство
![]()
Определение 2. Оператор А называется ограниченным, если существует такая константа М, что
![]()
для всех ![]()
Определение
3. Оператор А называется непрерывным,
если для любого ![]() существует такое число
существует такое число ![]() что из неравенства
что из неравенства
![]()
следует, что
![]()
В дальнейшем будут рассматриваться только линейные операторы.
В том случае, когда пространство R' представляет собой числовую прямую, оператор у = А(х) представляет собой функционал, а сформулированные определения линейности, непрерывности и ограниченности переходят в соответствующие определения, введенные для функционалов в § 23.
Следующая теорема представляет собой обобщение теоремы 1 § 23.
Теорема 1. Для линейного оператора непрерывность и ограниченность эквивалентны.
Доказательство. 1. Пусть оператор
А ограничен. Из неравенства ![]() следует, что
следует, что
![]() (1)
(1)
где М — константа, входящая в
определение ограниченности. Если взять ![]() то неравенство
(1) дает
то неравенство
(1) дает ![]() т.е. оператор А непрерывен.
т.е. оператор А непрерывен.
2. Пусть оператор А непрерывен. Ограниченность его будем доказывать от противного. Предположим, что оператор А неограничен. Тогда существует такая последовательность:
![]() (2)
(2)
что
![]()
Положим
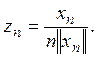
Очевидно, что ![]() т.е.
т.е. ![]() при
при ![]() Рассмотрим последовательность
Рассмотрим последовательность
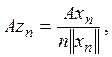
являющуюся образом последовательности ![]() Норма всех элементов
Норма всех элементов ![]() не менее единицы:
не менее единицы:
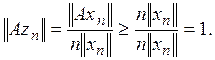
Так как для каждого линейного оператора
![]()
a ![]() получаем
противоречие с предположением о непрерывности оператора. Следовательно, оператор
А должен быть ограниченным.
получаем
противоречие с предположением о непрерывности оператора. Следовательно, оператор
А должен быть ограниченным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.