Линейные нормированные пространства, страница 11

                                              (8)

По определению обратного оператора,

откуда, умножая эти равенства на  и  соответственно и складывая, получим:

С другой стороны, из (8) и из определения обратного оператора следует, что

что вместе с предыдущим равенством дает

Теорема 6. Если Т — линейный ограниченный обратимый оператор, то оператор  ограничен.

Для доказательства теоремы нужны следующие две леммы:

Лемма 1. Пусть М — всюду плотное множество в банаховом пространстве Е. Тогда любой элемент  можно разложить в ряд

где  причем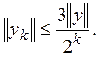

Доказательство. Строим последовательность элементов  следующим образом:  выберем так, чтобы было

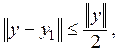                                                             (9)

что возможно, так как неравенство (9) определяет сферу радиуса  с центром в точке у, внутри которой должен найтись элемент на М (М всюду плотно в Е). Выберем  так, чтобы 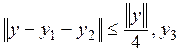 так, чтобы 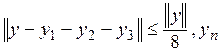 так, чтобы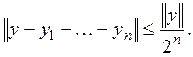

Такой выбор всегда возможен, так как М всюду плотно в Е. В силу выбора элементов

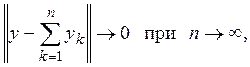
т. е. ряд 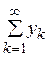 сходится к у.

Оценим нормы элементов

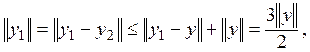
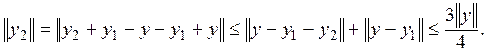
Наконец, получим:

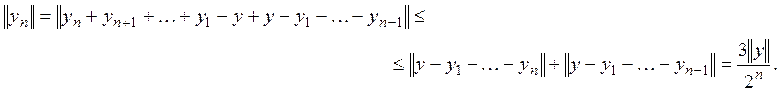Лемма доказана.

Лемма 2. Если банахово пространство Е есть сумма счетного количества множеств

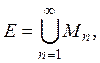
то хотя бы одно из этих множеств плотно в некоторой сфере.

Доказательство. Без ограничения общности можно считать, что

Предположим, что все они нигде не плотны, т. е. что внутри всякой сферы существует другая сфера, не содержащая ни одной точки

Возьмем произвольно сферу  в ней существует сфера  не содержащая ни одной точки  в  существует сфера  не содержащая ни одной точки  и т.д. Получим последовательность вложенных друг в друга сфер, причем сферы можно выбирать так, чтобы радиус сферы  стремился к нулю при  В банаховом пространстве такие сферы имеют общую точку. Эта точка есть элемент из Е, но он не принадлежит ни одному из множеств  что противоречит условию леммы. Лемма доказана.

Доказательство теоремы 6. В пространстве  рассмотрим множества  где  — совокупность у, для которых выполняется неравенство

Всякий элемент  попадает в некоторое  т. е. 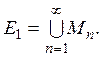 По второй лемме хоть одно из  плотно в некоторой сфере  Внутри сферы  рассмотрим шаровой слой Р — совокупность точек z, для которых справедливо неравенство

где

Параллельно перенеся шаровой слой Р так, чтобы его центр попал в начало координат, получим шаровой слой

Покажем, что в  плотно некоторое множество  Рассмотрим  тогда  Пусть, кроме того,  В силу выбора z

и  получим:

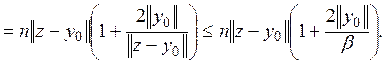
Величина 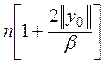 не зависит от z. Обозначим 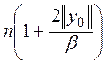 через N.

Тогда по определению  и  плотно в  так как  получено из  так же как и  из Р, сдвигом на  а  плотно в Р. Рассмотрим произвольный элемент у из  Всегда можно подобрать  так, чтобы, было  Для  можно построить последовательность  сходящуюся к  Тогда последовательность  сходится к у. (Очевидно, что если  то и  при любом действительном числовом множителе )

Мы доказали, что для любого  найдется сходящаяся к нему последовательность из элементов  т.е. что  всюду плотно в

Рассмотрим  по лемме 1 его можно разложить в ряд по элементам

причем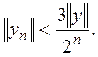

Рассмотрим в пространстве Е ряд, составленный из прообразов  т.е.

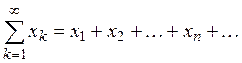
Этот ряд сходится к некоторому элементу х, так как имеет место неравенство 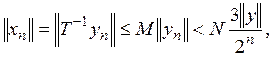 следовательно,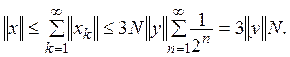

В силу сходимости ряда  и непрерывности Т можно применить Т ряду. Получим:

откуда  Мы имеем:

и так как оценка верна для любого у, то отсюда следует, что  ограничен.

Теорема 7. Оператор, близкий к обратимому, обратим, т. е. если  — линейный обратимый оператор, отображающий пространство Е в пространство  и  — оператор, также отображающий Е в  причем 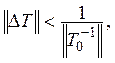 то оператор  обратим.

Доказательство. Пусть оператор Т переводит  в

Применив к этому равенству оператор  получим:

                                                    (10)

если обозначить  через z, а  через А, то уравнение (10) запишется в виде

|где А — оператор, отображающий банахово пространство Е в себя, причем

Отображение  есть сжатое отображение пространства Е в себя; следовательно, оно имеет единственную неподвижную точку, которая является единственным решением уравнения (10), а это и значит, что оператор Т обратим.