Линейные нормированные пространства, страница 7

и

    (ограниченность), т. е.  представляет собой ограниченный линейный функционал на  Будем наряду с записью f(x) пользоваться более симметричной записью:

                                                                   (1)

аналогичной обозначению скалярного произведения. При фиксированном  мы можем рассматривать это выражение как функционал на  а при фиксированном  — как функционал на R.

Отсюда следует, что для каждого элемента  норма определяется двумя способами: во-первых, определена его норма как элемента из R, а во-вторых — как линейного функционала на  т. е. как элемента из  Пусть  обозначает норму х как элемента из R, а  — норму х как элемента из  Покажем, что на самом деле  Пусть f — произвольный элемент из  Тогда

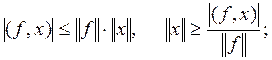
так как левая часть последнего неравенства не зависит от f, то

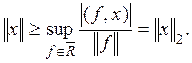
Но, согласно следствию из теоремы Хана-Банаха, для каждого элемента  найдется такой линейный функционал  что

Следовательно,

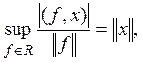
т.е

Итак, доказана следующая теорема.

Теорема. R изометрично некоторому линейному многообразию в

Так как мы условились не различать изометричные между собой пространства, то эту теорему можно сформулировать так:

В том случае, когда  пространство R называется рефлективным. Если  то R называется нерефлективным.

Конечномерные пространства  и пространство  являются примерами рефлективных пространств (для них даже ).

Пространство с сходящихся к нулю последовательностей дает пример полного нерефлективного пространства. Действительно, выше (§ 24, примеры 2 и 3) мы установили, что сопряженным к с является пространство l числовых последовательностей  удовлетворяющих условию 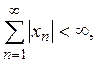 которому в свою очередь сопряжено пространство т всех ограниченных последовательностей. Пространства с и m не изометричны. Это следует уже из того, что с сепарабельно, a m — нет. Таким образом, с нерефлективно.

Пространство  непрерывных функций на некотором отрезке [а, b] также нерефлективно. Мы, однако, не будем останавливаться на доказательстве этого утверждения[1].

Московский математик А. И. Плеснер установил, что для любого нормированного пространства R существуют только две возможности:

или пространство R рефлективно, т. е.

или пространства  все различны.

Пространство  представляет собой пример рефлективного пространства (так как  где  то ).

§ 27. Слабая сходимость

Во многих вопросах анализа важную роль играет понятие так называемой слабой сходимости элементов линейного нормированного пространства.

Определение. Последовательность  элементов линейного нормированного пространства R называется слабо сходящейся к элементу х, если:

1) нормы элементов  ограничены в совокупности[2]:

2) для всякого

Условие 2 может быть несколько ослаблено; именно справедлива следующая

Теорема. Последовательность  слабо сходится к элементу х, если:

1)

2)  для всякого  где  — некоторое множество, линейная оболочка которого всюду плотна в

Доказательство. Из условий теоремы и определения линейного функционала следует, что если  — линейная комбинация элементов из  то

Пусть теперь  — произвольный линейный функционал на R и  -сходящаяся к  последовательность функционалов, каждый из которых представляет собой линейную комбинацию элементов из . Покажем, что  Пусть М таково, что

Оценим разность  Так как  то для любого  найдется такое К, что для всех k > К.

откуда получаем:

Но по условию  при  Следовательно,

Если последовательность  сходится к х по норме, т.е. если  при  то такую сходимость часто в отличие от слабой сходимости называют сильной сходимостью.

Если некоторая последовательность  сходится к х сильно, то она сходится к тому же самому пределу и слабо. Действительно, если  то для любого линейного функционала f имеем:

Обратное, вообще говоря, неверно: из слабой сходимости сильная сходимость не вытекает. Например, в пространстве  последовательность векторов

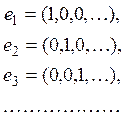
слабо сходится к нулю. Действительно, всякий линейный функционал f в  записывается как скалярное произведение на некоторый фиксированный вектор