Линейные нормированные пространства, страница 12

Теорема 8. Оператор, обратный оператору  где I — тождественный оператор, а оператор А имеет норму меньше 1 (), представляется в виде

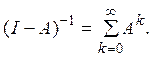
Доказательство. Рассмотрим преобразование пространства Е в себя:

Отображение  есть сжатое отображение пространства Е в себя в силу условия

Решаем уравнение  итерациями:  Полагая  получим:

Переходим к пределу при  тогда  стремится к единственному решению уравнения  т. е. 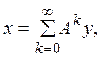 откуда

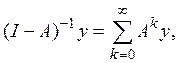
что и дает равенство (11).

4. Сопряженные операторы

Рассмотрим линейный оператор  отображающий банахово пространство Е в банахово пространство  Пусть  — линейный функционал, определенный на  т.е.  Применим функционал g к элементу  как легко проверить, есть линейный функционал, определенный на Е; обозначим его f(x). Функционал f(x) есть, таким образом, элемент пространства  Каждому функционалу  мы поставили в соответствие функционал  т. е. получили некоторый оператор, отображающий  в Е. Этот оператор называется сопряженным оператору A и обозначается А* или

Воспользовавшись для функционала f(x) обозначением  получим  или  Это соотношение можно принять за определение сопряженного оператора.

Пример. Выражение сопряженного оператора в конечномерном пространстве. Пространство  (n-мерное) отображается в пространство  (m-мерное) оператором А. Оператор А задается матрицей ().

Отображение у = Ах можно записать в виде системы

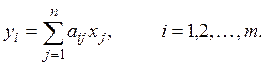
Оператор f(x) можно записать в виде

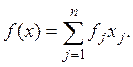
Из равенства

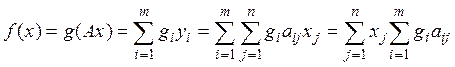
получим 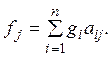 Так как  отсюда следует, что оператор А* задается матрицей, транспонированной матрице оператора А. Укажем основные свойства сопряженных операторов.

1. Оператор, сопряженный с суммой двух линейных операторов, равен сумме сопряженных операторов;

Пусть  или  тогда   откуда

2. Оператор, сопряженный с оператором kА, где k — числовой множитель, равен оператору, сопряженному с А, умноженному на k:

Проверка данного свойства элементарна.

3. Единичный оператор самосопряжен.

Теорема 9. Оператор А*, сопряженный с линейным оператором А, отображающим банахово пространство Е в банахово пространство  также линеен, причем

Доказательство. Линейность оператора А* очевидна. Докажем равенство норм. В силу свойств нормы оператора имеем:

откуда  или  следовательно,

Возьмем  и образуем 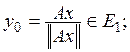 очевидно, что  По следствию из теоремы Хана-Банаха существует функционал , такой, что  и  т.е.

Из неравенства  получим  что вместе с неравенством (12) дает:

Добавление к главе III Обобщенные функции

В ряде случаев в анализе и в различных его приложениях, например в теоретической физике, возникает потребность в введении, наряду с «обычными» функциями тех или иных «обобщенных» функций, типичным примером которых является хорошо известная -функция, уже упоминавшаяся нами выше (§ 23, пример 4).

Необходимо сразу же подчеркнуть, что те понятия, на которых мы вкратце остановимся в этом добавлении, возникли вовсе не в результате стремления к расширению понятий анализа лишь ради самого этого расширения, а были вызваны совершенно конкретными задачами. Более того, эти понятия по существу использовались физиками уже довольно давно, во всяком случае раньше, чем они привлекли внимание математиков.

Тот способ введения обобщенных функций, о которых будет идти речь ниже, ведет свое начало от работ С. Л. Соболева, опубликованных в 1935-1936 гг. Позже эти идеи развиты, в несколько расширенном виде, Л. Шварцем.

Рассмотрим на прямой совокупность (D) функций  каждая из которых равна нулю вне некоторого интервала (для каждой  — своего) и имеет производные всех порядков. Элементы из (D) можно обычным образом складывать между собой и умножать на числа. Таким образом, D представляет собой линейное пространство. Норму в этом пространстве мы не будем вводить, однако в D можно естественным образом определить понятие сходимости последовательности элементов, а именно: мы скажем, что  если: 1) существует интервал, вне которого все  и  равны нулю, и 2) последовательность производных  порядка[4] k (k = 0, 1, 2, ...) на этом интервале равномерно сходится к  Тот факт, что это понятие сходимости не связано ни с какой нормой, не вызовет никаких неудобств. Введем теперь понятие обобщенной функции.