Линейные нормированные пространства, страница 14

в котором производная  уже никак не участвует.

Эти соображения приводят нас к следующему определению.

Определение 3. Пусть T — некоторая обобщенная функция. Ее производной  называется функционал, определяемый формулой

Ясно, что  имеет смысл для всех  и представляет собой обобщенную функцию.

Аналогично определяются производные второго, третьего и т. д. порядков.

Непосредственно из определения вытекает справедливость следующих утверждений:

Теорема 1. Всякая обобщенная функция имеет производные всех порядков.

Теорема 2. Если последовательность  сходится к обобщенной функции Т (в смысле определения 2), то последовательность производных  сходится к  Иными словами: всякий сходящийся ряд обобщенных функций можно дифференцировать почленно любое число раз.

Теперь видно, что тот функционал  (см. пример 3), который мы назвали производной от -функции, действительно является производной от  в смысле определения 3.

Замечание. Понятие производной от обобщенной функции можно ввести еще несколько иным путем. Именно, определим сдвиг  функционала Т (где h - произвольное число), положив

(например,  и т.д.). Тогда нетрудно проверить, что предел

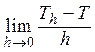
существует и равен производной  функционала Т.

4. Если функционал  определяется некоторой дифференцируемой функцией  то функционал  определяется функцией  т. е. обобщенная производная от функции совпадает с ее обычной производной, если последняя существует.

5. Пусть Т определяется функцией

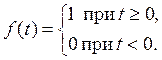
Тогда

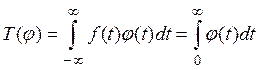
и

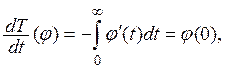
т. е.  есть -функция.

6. Если f(t) — кусочно-непрерывная функция, имеющая производную во всех точках непрерывности, то ее обобщенная производная в точках непрерывности совпадает с ее обычной производной, а в каждой точке разрыва  она равна -функции умноженной на величину скачка функции в этой точке.

7. Положим

                                                          (3)

обобщенная производная этой функции равна

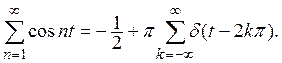
Подчеркнем, что ряд, стоящий слева, сходится в том смысле, как мы определили понятие сходимости для обобщенных функций (определение 2). Ряд (3) I можно продифференцировать почленно любое число раз.

Последний пример показывает, что понятие обобщенной функции позволяет приписать некоторый вполне определенный смысл сумме ряда, который в обычном смысле расходится. То же самое относится и ко многим расходящимся интегралам. С этим обстоятельством часто приходится встречаться в теоретической физике, где в каждом отдельном случае для придания определенного смысла расходящемуся ряду или интегралу прибегают к различным частным приемам.

Аналогично тому, как выше мы определили обобщенные функции одного независимого переменного, можно ввести обобщенные функции нескольких независимых переменных. Для этого только в качестве исходного пространства D следует взять пространство всех бесконечное число раз дифференцируемых функций п независимых переменных, каждая из которых равна нулю вне некоторой сферы. Все введенные выше понятия автоматически переносятся на этот случай. Легко проверить, что всякая обобщенная функция нескольких независимых переменных имеет частные производные всех порядков, причем результат дифференцирования по нескольким переменным всегда не зависит от порядка дифференцирования.