Линейные нормированные пространства, страница 5

для любого

Произведением линейного функционала  на число  называется такой функционал  что

для любого

Легко проверить, что так определенные операции сложения функционалов и умножения их на числа удовлетворяют всем аксиомам линейного пространства. Кроме того, определенная нами выше норма линейного функционала удовлетворяет всем требованиям, содержащимся в определении линейного нормированного пространства. Действительно,

1)  для любого

2)

3)

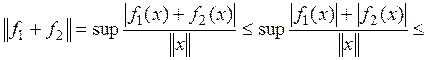
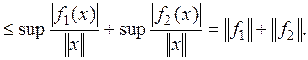
Таким образом, совокупность всех линейных функционалов на некотором нормированном пространстве R сама представляет собой линейное нормированное пространство; оно называется сопряженным к R и обозначается

Теорема 1. Сопряженное пространство всегда полно.

Доказательство. Пусть  — фундаментальная последовательность линейных функционалов. По определению фундаментальной последовательности, для каждого  найдется такое N, что  для ,всех п, т > N. Тогда для любого

т. е. при любом  числовая последовательность  сходится.

Положим

 представляет собой линейный функционал. Действительно,

l)

2) Выберем N так, что  для всех п > N. Тогда  для всех р. Следовательно,

Переходя к пределу при  получим:

т.е. функционал f(x) ограничен. Докажем теперь, что функционал f является пределом последовательности  По определению нормы, для всякого  найдется такой элемент  что

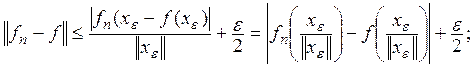
так как

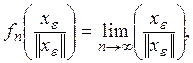
то можно найти такое  что-при

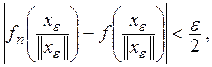
так что для  будет выполнено неравенство

Теорема доказана.

Подчеркнем еще раз, что эта теорема справедлива независимо от того, полно или нет исходное пространство R.

Примеры. 1. Пусть пространство Е конечномерное, с базисом  Тогда функционал f(x) выражается в виде

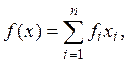                                                          (1)

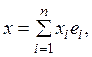где  а

Таким образом, функционал определяется п числами,  — его значениями на базисных векторах. Пространство, сопряженное с конечномерным, также конечномерное и имеет ту же размерность.

Норма в сопряженном пространстве определяется в соответствии с тем, какова норма в пространстве Е.

а) Пусть  Было показано, что тогда

т. е. пространство, сопряженное с евклидовым, само евклидово.

б) Пусть  Тогда

Отсюда следует, что

Норма  не может быть меньше, чем  так как, если положить

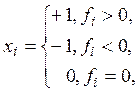
будет выполнено равенство

в) Если  то  причем

Это следует из неравенства Гельдера

и из того, что знак равенства достигается (при ).

2. Рассмотрим пространство с, состоящее из последовательностей  таких, что  при  где

Если функционал в пространстве с выражается формулой

                                          (2)

он имеет норму

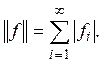
Неравенство 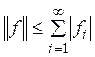 очевидно. С другой стороны, если 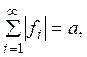 то для всякого  можно найти такое N, что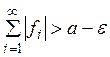

Положим теперь

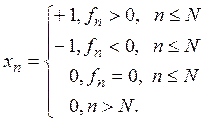
Тогда

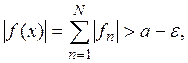
откуда следует, что

Докажем, что в пространстве с все функционалы имеют вид (2). Положим

т. е.  означает последовательность, в которой на n-м месте стоит единица, а на остальных — нули.

Пусть задан функционал  обозначим через  Если

                                                    (3)

то

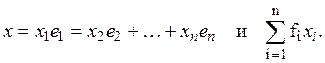
Сумма 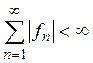 для всякого линейного ограниченного функционала. Если бы было 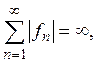 то для всякого Н можно было бы найти такое N, что

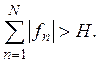
Построим элемент х следующим образом:

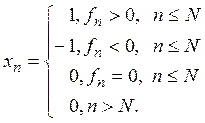
Норма такого элемента равна единице, а

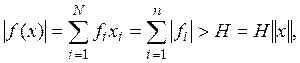
что противоречит предположению об ограниченности функционала.

Множество элементов вида (3) всюду плотно в пространстве с. Поэтому линейный непрерывный функционал однозначно определяется своими значениями на этом множестве. Таким образом, для всякого х

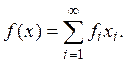
Пространство, сопряженное с пространством с, состоит из последовательностей  удовлетворяющих условию

3. Пусть пространство состоит из последовательностей

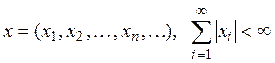
с нормой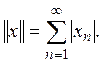

Можно доказать, что сопряженным с этим пространством является пространство ограниченных последовательностей

с нормой

Во всех примерах, приведенных для конечномерных пространств, пространство, сопряженное с сопряженным, совпадало с исходным. Это всегда имеет место в конечномерном случае. Однако, как показывают примеры 2 и 3, в бесконечномерном случае пространство, сопряженное с сопряженным, может и не совпадать с исходным.