Другие предметы \ Функциональный анализ

Линейные нормированные пространства, страница 10

Пример. Общий вид линейного оператора, переводящего конечномерное пространство в конечномерное. Имеется n-мерное пространство с базисом Всякая точка этого пространства записывается в виде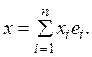

Линейный оператор А отображает в конечномерное пространство с базисом

Рассмотрим разложение по этому базису образов базисных векторов пространства :

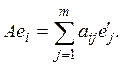
Пусть теперь у = Ах,

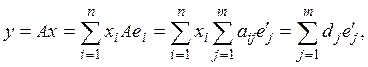
где

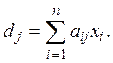(3)

Из формулы (З) видно, что для задания оператора А достаточно задать матрицу коэффициентов

Линейный оператор не может отображать конечномерного пространства на пространство большего числа измерений, так как все линейные соотношения между элементами сохраняются для их образов.

2. Норма оператора. Сумма и произведение операторов. Произведение оператора на число

Определение 4. Пусть А — линейный ограниченный оператор. Это означает, что существуют такие числа М, что

(4)

для всех

Нормой оператора А называется нижняя грань чисел М, удовлетворяющих условию (4).

Из определения нормы оператора следует, что

Если же то существует такой элемент х, что

Теорема 2. Для любого линейного ограниченного оператора

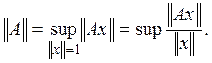
Доказательство. Введем обозначение

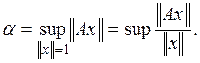
Докажем сначала, что

Так как 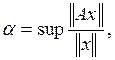для любого существует такой элемент что

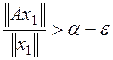
или

откуда следует, что

и, так как произвольно,

Знака неравенства быть не может. Действительно, пусть

Тогда

Но отсюда вытекает, что, какова бы ни была точка х, имеют место неравенства

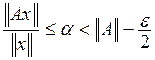
или

т. е. не есть нижняя грань тех М, для которых

Из полученного противоречия видно, что

В дальнейшем мы будем пользоваться полученным выражением для нормы оператора наравне с первоначальным определением нормы.

Определение 5. Пусть имеется два линейных непрерывных оператора и переводящих банахово пространство Е в банахово пространство Назовем суммой этих двух операторов оператор А, ставящий в соответствие элементу элемент определяемый по формуле

Легко проверить, что также является линейным оператором

Теорема 3. Между нормами операторов и существует соотношение

(5)

Доказательство. Очевидно, что

откуда следует неравенство (5).

Определение 6. Пусть и — линейные непрерывные операторы, причем переводит банахово пространство Е в банахово пространство a переводит банахово пространство в банахово пространство Произведением операторов и (обозначается ) называется оператор, ставящий элементу в соответствие элемент причем

Теорема 4. Если то

(6)

Доказательство.

откуда следует утверждение теоремы.

Сумма и произведение трех и более операторов определяются последовательно. Обе операции ассоциативны.

Произведение оператора А на действительное число k (обозначается kА) определяется следующим образом: оператор kА ставит в соответствие элементу элемент из пространства

Легко проверить, что по отношению ко введенным операциям сложения и умножения на число ограниченные линейные операторы образуют линейное пространство. Введя норму оператора, как было указано выше, можно это линейное пространство сделать нормированным.

Упражнение. Доказать, что пространство ограниченных линейных операторов, отображающих пространство в полное пространство полно.