![]()
поэтому
![]()
Так как ![]() при
при ![]() для всякого
для всякого ![]() то
то
![]()
для каждого линейного функционала в ![]()
В то же время в сильном
смысле последовательность ![]() ни к какому пределу не
сходится.
ни к какому пределу не
сходится.
Посмотрим, что означает слабая сходимость в некоторых конкретных пространствах.
Примеры. 1. В конечномерном пространстве ![]() слабая сходимость совпадает с сильной. Действительно,
рассмотрим функционалы, соответствующие умножению на элементы
слабая сходимость совпадает с сильной. Действительно,
рассмотрим функционалы, соответствующие умножению на элементы
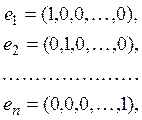
Пусть ![]() слабо
сходится к х. Тогда
слабо
сходится к х. Тогда
![]()
т.е. первые координаты векторов ![]() стремятся к первой координате вектора х,
их вторые координаты стремятся ко второй координате вектора х и т. д. Но
тогда
стремятся к первой координате вектора х,
их вторые координаты стремятся ко второй координате вектора х и т. д. Но
тогда
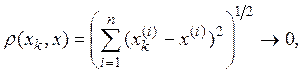
т. е. ![]() сильно
сходится к х. Так как из сильной сходимости всегда следует слабая, то наше
утверждение доказано.
сильно
сходится к х. Так как из сильной сходимости всегда следует слабая, то наше
утверждение доказано.
2. Слабая сходимость в ![]() В
качестве множества
В
качестве множества ![]() линейные комбинации элементов которого
всюду плотны в
линейные комбинации элементов которого
всюду плотны в ![]() можно взять совокупность
векторов
можно взять совокупность
векторов
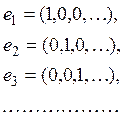
Если
![]()
— произвольный вектор из ![]() то принимаемые на х значения
соответствующих линейных функционалов равны
то принимаемые на х значения
соответствующих линейных функционалов равны
![]()
т.е. координатам вектора х. Следовательно,
слабая сходимость последовательности ![]() в
в ![]() означает, что числовая последовательность k-х координат этих векторов
означает, что числовая последовательность k-х координат этих векторов ![]() сходится.
Выше мы видели, что эта сходимость не совпадает с сильной сходимостью в
сходится.
Выше мы видели, что эта сходимость не совпадает с сильной сходимостью в ![]()
3. Слабая сходимость в пространстве непрерывных функций. Пусть
![]() пространство непрерывных функций на
отрезке [а, b]. Можно показать, что совокупность
пространство непрерывных функций на
отрезке [а, b]. Можно показать, что совокупность ![]() всех
линейных функционалов
всех
линейных функционалов ![]() каждый из которых определяется
как значение функции в некоторой фиксированной точке
каждый из которых определяется
как значение функции в некоторой фиксированной точке ![]() (см.
пример 4 § 23), обладает тем свойством, что если последовательность
(см.
пример 4 § 23), обладает тем свойством, что если последовательность ![]() ограничена и
ограничена и ![]() для
всех
для
всех ![]() то
то ![]() слабо
сходится x(t). Для каждого такого
функционала
слабо
сходится x(t). Для каждого такого
функционала ![]() условие
условие
![]()
означает, что
![]()
Таким образом, слабая сходимость последовательности непрерывных функций означает, что эта последовательность а) равномерно ограничена, б) сходится в каждой точке.
Ясно, что эта сходимость
не совпадает со сходимостью по норме в ![]() т. е. с
равномерной сходимостью непрерывных функций (приведите соответствующий пример).
т. е. с
равномерной сходимостью непрерывных функций (приведите соответствующий пример).
Аналогично понятию слабой сходимости элементов линейного нормированного пространства R можно ввести понятие слабой сходимости линейных функционалов.
Определение.
Последовательность линейных функционалов ![]() называется слабо сходящейся к линейному
функционалу f, если:
называется слабо сходящейся к линейному
функционалу f, если:
1) ![]() ограничены
в совокупности
ограничены
в совокупности ![]()
2) для всякого элемента ![]()
![]()
![]()
Слабая сходимость линейных
функционалов обладает свойствами, аналогичными указанным выше свойствам слабой
сходимости элементов, а именно из сильной сходимости (т.е. сходимости по норме)
линейных функционалов следует их слабая сходимость, и выполнение условия ![]() достаточно требовать не для всех
достаточно требовать не для всех ![]() а только для совокупности элементов,
линейные комбинации которых всюду плотны в R.
а только для совокупности элементов,
линейные комбинации которых всюду плотны в R.
Рассмотрим один важный
пример слабой сходимости линейных функционалов. Выше (§23, пример 4) мы
говорили о том, что «![]() -функцию», т.е. функционал на
-функцию», т.е. функционал на ![]() который каждой непрерывной функции ставит
в соответствие ее значение в точка нуль[3],
можно «в некотором смысле» рассматривать как предел «обычных» функций, каждая
из которых обращается в нуль вне некоторой малой окрестности нуля и имеет
интеграл, равный 1. Сейчас мы можем уточнить это утверждение. Пусть
который каждой непрерывной функции ставит
в соответствие ее значение в точка нуль[3],
можно «в некотором смысле» рассматривать как предел «обычных» функций, каждая
из которых обращается в нуль вне некоторой малой окрестности нуля и имеет
интеграл, равный 1. Сейчас мы можем уточнить это утверждение. Пусть ![]() последовательность
непрерывных функций, удовлетворяющих следующим условиям:
последовательность
непрерывных функций, удовлетворяющих следующим условиям:
![]() (1)
(1)
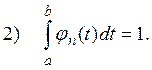
Тогда для любой непрерывной на отрезке [a, b] функции x(t) имеем:
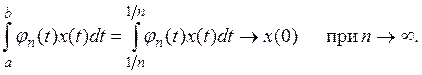
Действительно, по теореме о среднем
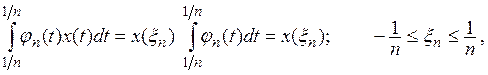
если ![]() то
то ![]() и
и ![]()
Выражение
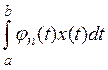
представляет собой линейный функционал на пространстве
непрерывных функций. Таким образом, полученный нами результат можно
сформулировать следующим образом: ![]() -функция есть предел, в
смысле слабой сходимости линейных функционалов, последовательности (1).
-функция есть предел, в
смысле слабой сходимости линейных функционалов, последовательности (1).
В различных применениях понятия слабой сходимости линейных функционалов важную роль играет следующая
Теорема 1. Если линейное нормированное пространство R сепарабельно, то в любой ограниченной последовательности линейных функционалов на R содержится слабо сходящаяся подпоследовательность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.