Среди различных линейных нормированных
пространств, встречающихся в функциональном анализе, одним из важнейших
является гильбертово пространство, названное так по имени немецкого математика
Д.Гильберта, который ввел это пространство в связи со своими исследованиями по
теории интегральных уравнений. Оно является естественным бесконечномерным
аналогом n-мерного евклидова пространства. С одной из возможных
реализаций гильбертова пространства мы уже познакомились в гл. III, ч. I – это пространство
![]() элементами которого являются числовые
последовательности,
элементами которого являются числовые
последовательности,
![]()
удовлетворяющие условию
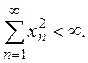
Понятие интеграла Лебега позволяет ввести
другую, в некоторых случаях более удобную, реализацию того же самого
пространства – пространство функций с интегрируемым квадратом. В этой главе мы
рассмотрим определение и основные свойства пространства функций с интегрируемым
квадратом и установим его изометричность (при соответствующих предположениях
относительно той меры, по которой производится интегрирование) с пространством ![]() .
.
В следующей главе будет дано аксиоматическое определение гильбертова пространства.
Ниже мы рассматриваем функции f(x) определенные
на некотором множестве R, с заданной на нем
мерой ![]() удовлетворяющей условию
удовлетворяющей условию ![]() Функции f(x) предполагаются измеримыми и определенными почти всюду на R. Функции, эквивалентные на R, мы не будем различать. Вместо
Функции f(x) предполагаются измеримыми и определенными почти всюду на R. Функции, эквивалентные на R, мы не будем различать. Вместо ![]() будем
для краткости писать просто
будем
для краткости писать просто ![]()
Определение 1. Говорят, что f(x) есть функция с интегрируемым (или суммируемым) квадратом на R, если интеграл
![]()
существует (конечен). Совокупность всех функций с интегрируемым квадратом на R обозначим L2.
Установим основные свойства таких функций.
Теорема 1. Произведение двух функций с интегрируемым квадратом есть интегрируемая функция.
Доказательство непосредственно вытекает из неравенства
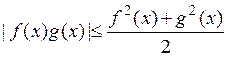
и свойств интеграла Лебега.
Следствие 1. Всякая функция f(x) с интегрируемым квадратом интегрируема.
Действительно,
достаточно в теореме 1 положить ![]()
Теорема 2. Сумма двух функций из L2 также принадлежит L2.
Доказательство. Действительно,
![]()
и, в силу теоремы 1, каждая из трех функций, стоящих справа, суммируема.
Теорема 3. Если ![]() и а – произвольное
число, то
и а – произвольное
число, то ![]()
Доказательство.
Если ![]() то
то
![]()
Теоремы 2 и 3 показывают, что линейные комбинации функций из L2 снова принадлежат L2; при этом очевидно, что сложение функций из L2 и умножение их на числа удовлетворяют всем условиям 1-8, перечисленным в определении линейного пространства (гл. III §24), иначе говоря, класс L2функций с суммируемым квадратом представляет собой линейное пространство.
Определим теперь для функций из L2скалярное произведение, положив
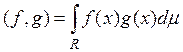 (1)
(1)
Как известно, скалярным произведением называется любая числовая функция пары векторов линейного пространства, удовлетворяющая следующим условиям:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Из основных свойств интеграла сразу следует,
что условиям 1-3 выражение (1) действительно удовлетворяет. Поскольку же мы
условились не различать эквивалентные между собой функции (и, в частности, за нулевой
элемент считать совокупность всех функций на R, эквивалентных ![]() ), то условие 4) будет
также выполнено (см. следствие из теоремы 9 § 43). Мы приходим, таким образом,
к следующему определению.
), то условие 4) будет
также выполнено (см. следствие из теоремы 9 § 43). Мы приходим, таким образом,
к следующему определению.
Определение 2. Пространством L2 называется евклидово пространство[1], элементами которого являются классы эквивалентных между собой функций с интегрируемым квадратом, сложение элементов и умножение их на числа определяются как обычное сложение и умножение функций, а скалярное произведение определяется формулой
![]() (1)
(1)
В L2, как и во всяком евклидовом пространстве, выполнено неравенство Коши-Буняковского, которое в данном случае имеет вид:
![]() (2)
(2)
и неравенство треугольника, имеющее вид:
![]() (3)
(3)
В частности, при ![]() неравенство
Коши-Буняковского дает следующее полезное неравенство:
неравенство
Коши-Буняковского дает следующее полезное неравенство:
![]() (4)
(4)
Введем в L2норму, положив
![]() (5)
(5)
Упражнение. Исходя из свойств 1-4 скалярного произведения, доказать, что норма, определенная равенством (5), удовлетворяет условиям 1–3 определения нормы (§21).
Весьма важную роль во многих вопросах анализа играет следующая
Теорема 4. Пространство L2 полно.
Доказательство. а) Пусть {fn(x)} – фундаментальная последовательность в L2, т. е.
![]()
Тогда можно выбрать подпоследовательность индексов {nk} так, что
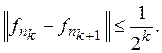
Отсюда, согласно неравенству (4), вытекает, что
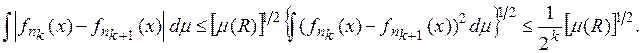
Из этого неравенства и теоремы 2 § 44 (следствие) вытекает, что ряд
![]()
сходится почти всюду на R. Тогда и ряд
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.