Нетрудно убедиться на примерах, что из
сходимости в среднем некоторой последовательности не вытекает, что сама эта
последовательность сходится почти всюду. Действительно, последовательность
функций ![]() построенная на стр. 233, сходится, очевидно,
в среднем к функции
построенная на стр. 233, сходится, очевидно,
в среднем к функции ![]() но при этом, как показано там
же, не сходится почти всюду. Покажем теперь, что из сходимости почти всюду (и
даже всюду) не вытекает сходимость в среднем. Пусть
но при этом, как показано там
же, не сходится почти всюду. Покажем теперь, что из сходимости почти всюду (и
даже всюду) не вытекает сходимость в среднем. Пусть
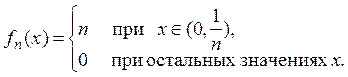
Ясно, что последовательность {fn(x)} сходится к 0 всюду на [0,1], но в то же время
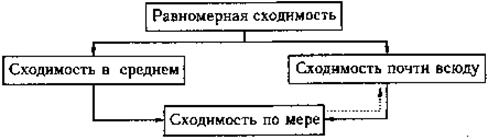
Из неравенства Чебышева (§43, теорема 9) следует, что если последовательность сходится в среднем, то она сходится и по мере. Поэтому теорема 3, которую мы здесь доказали независимо, вытекает из теоремы 4 §41. Соотношения между различными типами сходимости функций показаны на схеме, где пунктирная стрелка означает возможность выбора из последовательности, сходящейся по мере, подпоследовательности, сходящейся почти всюду.
Пространство L2функций с интегрируемым
квадратом зависит, вообще говоря, от выбора пространства R и меры ![]() Полное его обозначение
должно было бы быть
Полное его обозначение
должно было бы быть ![]() Только в исключительных случаях
пространство
Только в исключительных случаях
пространство ![]() конечномерно. Наибольшее значение в
анализе имеют те пространства,
конечномерно. Наибольшее значение в
анализе имеют те пространства, ![]() которые в некотором,
выясняемом далее, смысле счетномерны.
которые в некотором,
выясняемом далее, смысле счетномерны.
Для того чтобы охарактеризовать эти пространства, нам понадобится еще одно понятие, относящееся к теории меры.
В совокупности M измеримых подмножеств пространства R (меру которого мы предположили конечной) можно ввести расстояние, положив
![]()
Если мы будем отождествлять такие множества А
и В, для которых ![]() (т. е., иначе говоря,
будем рассматривать не отдельные множества, а классы множеств, совпадающих с
точностью до множества меры 0), то множество M с расстоянием
(т. е., иначе говоря,
будем рассматривать не отдельные множества, а классы множеств, совпадающих с
точностью до множества меры 0), то множество M с расстоянием ![]() будет удовлетворять
всем аксиомам метрического пространства.
будет удовлетворять
всем аксиомам метрического пространства.
Определение 1. Мера называется имеющей счетный базис, если в метрическом пространстве M существует счетное всюду плотное множество.
Иначе говоря, мера ![]() имеет счетный базис, если существует такая
счетная система
имеет счетный базис, если существует такая
счетная система
![]()
измеримых подмножеств пространства R (счетный базис меры ![]() ), что
для любого измеримого
), что
для любого измеримого ![]() и любого
и любого ![]() найдется
такое
найдется
такое ![]() что
что
![]()
В частности, мера ![]() имеет,
очевидно, счетный базис, если ее можно представить как продолжение меры,
определенной на счетной системе множеств
имеет,
очевидно, счетный базис, если ее можно представить как продолжение меры,
определенной на счетной системе множеств ![]() В самом
деле, в этом случае кольцо
В самом
деле, в этом случае кольцо ![]() (оно, очевидно, счетно)
и представляет собой, в силу теоремы 3 § 38, искомый базис.
(оно, очевидно, счетно)
и представляет собой, в силу теоремы 3 § 38, искомый базис.
В частности, мера Лебега на отрезке числовой прямой порождается системой интервалов с рациональными концами в качестве элементарных множеств. Так как множество таких интервалов счетно, то мера Лебега обладает счетным базисом.
Произведение ![]() двух
мер со счетными базисами также обладает счетным базисом, так как конечные суммы
попарных произведений элементов базиса меры
двух
мер со счетными базисами также обладает счетным базисом, так как конечные суммы
попарных произведений элементов базиса меры ![]() на
элементы базиса меры
на
элементы базиса меры ![]() образуют, как легко проверить,
базис меры
образуют, как легко проверить,
базис меры ![]() Поэтому мера Лебега на плоскости (а также
и в n-мерном пространстве) имеет счетный базис.
Поэтому мера Лебега на плоскости (а также
и в n-мерном пространстве) имеет счетный базис.
Пусть
![]() (1)
(1)
есть счетный базис меры Легко видеть, что, расширяя
систему множеств (1), можно образовать счетный базис меры ![]()
![]() (2)
(2)
удовлетворяющий следующим условиям:
1) система множеств (2) замкнута по отношению к вычитанию;
2) система множеств (2) содержит R.
Из условий 1) и 2) вытекает, что система (2) замкнута по отношению к операциям взятия суммы и пересечения множеств в конечном числе.
Это следует из очевидных равенств
![]()
![]()
Теорема. Если мера ![]() имеет
счетный базис, то в
имеет
счетный базис, то в ![]() существует счетное всюду плотное
множество функций
существует счетное всюду плотное
множество функций
![]()
Доказательство. В качестве такого базиса в ![]() можно
выбрать конечные суммы
можно
выбрать конечные суммы
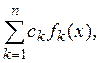 (3)
(3)
где ![]() – рациональные числа, а
– рациональные числа, а
![]() – характеристические функции элементов
счетного базиса меры
– характеристические функции элементов
счетного базиса меры ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.