Функции с интегрируемым квадратом, страница 4

Действительно, как мы уже показали в предыдущем параграфе, множество ступенчатых функций, принимающих лишь конечное число различных значений, всюду плотно в L₂. Так как очевидно, что любую функцию этого множества можно сколь угодно близко аппроксимировать функцией того же вида, но принимающей лишь рациональные значения, и так как множество функций вида (3) счетно, то для доказательства нашего утверждения достаточно показать, что любую ступенчатую функцию f(x), принимающую значения

на множествах

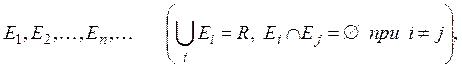
можно сколь угодно близко аппроксимировать в смысле метрики L₂функцией вида (3). Согласно сделанному замечанию, можно без ограничения общности предполагать, что наш базис меры  удовлетворяет условиям 1) и 2).

По определению счетного базиса меры  при любом  существуют такие множества  из нашего базиса меры  что  т.е.

Положим

и определим

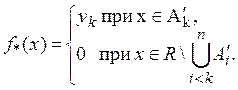
Легко видеть, что при достаточно малом  величина

сколь угодно мала и, следовательно, интеграл

сколь угодно мал при достаточно малом

В силу сделанных нами предположений относительно базиса меры  функция  есть функция вида (3). Теорема доказана.

Для того частного случая, когда R есть сегмент числовой прямой, a  – мера Лебега, счетный базис в  можно получить и более классическим способом: за такой базис можно, например, взять множество всех многочленов с рациональными коэффициентами. Оно всюду плотно (даже в смысле равномерной сходимости) во множестве непрерывных функций, а эти последние образуют всюду плотное множество в

В дальнейшем мы ограничимся рассмотрением пространств имеющих счетное всюду плотное множество (иными словами, являющихся сепарабельными – см. § 9).

§ 53. Ортогональные системы функций. Ортогонализация

В этом параграфе мы будем рассматривать функции  заданные на некотором измеримом множестве R с мерой  которую мы будем предполагать имеющей счетный базис и удовлетворяющей условию  Эквивалентные между собой функции мы по-прежнему не будем различать.

Определение 1. Система функций

                                                      (1)

называется линейно зависимой, если существуют такие постоянные  не все равные нулю, что

                                            (2)

почти всюду на R. Если же из (2) следует, что

то система (1) называется линейно независимой.

Ясно, что линейно независимая система не может содержать функции, эквивалентной

Определение 2. Бесконечная система функций

                                                  (4)

называется линейно независимой, если линейно независима любая ее конечная часть. Обозначим

множество всех конечных линейных комбинаций функций системы (4). Это множество называется линейной оболочкой системы (4). Через

обозначим замыкание множества М в пространстве L₂.  называется замкнутой линейной оболочкой системы (4).

Легко видеть, что множество М состоит из тех и только тех функций  которые можно аппроксимировать конечными линейными комбинациями функций системы (4) с любой наперед заданной точностью.

Определение 3. Система функций (4) называется полной, если для нее

Пусть в пространстве L₂существует счетное всюду плотное множество функций

Удаляя из этой системы те функции, которые линейно зависят от предыдущих, мы придем к линейно независимой системе функций

которая, как легко видеть, полна.

В случае, если в L₂ существует конечная полная система (1) линейно независимых функций, то

есть n-мерное евклидово пространство.

Во всех интересных для анализа случаях пространство L₂ бесконечно-мерно.

Очевидно, что для того, чтобы система (4) была полна, достаточно, чтобы линейными комбинациями принадлежащих ей функций можно было бы аппроксимировать с любой точностью каждую, из функций, принадлежащих некоторому всюду плотному в L₂множеству.

Пусть R = [а, b] есть сегмент числовой прямой с обычной лебеговой мерой. Тогда система функций

                                                      (5)

полна в пространстве