Функции с интегрируемым квадратом, страница 5

Действительно, согласно теореме Вейерштрасса (см, например: Немыцкий, Слудская, Черкасов «Курс математического анализа», т. 2, гл. III § 3), линейные комбинации функций (5) плотны в совокупности всех непрерывных функций. Полнота системы (5) вытекает теперь из сделанного нами замечания и теоремы 2 § 51.

Функции f(x) и g(х) в L₂называются взаимно ортогональными, если

Всякую систему  отличных от нуля и попарно ортогональных функций из L₂мы будем называть ортогональной системой. Ортогональная система называется нормированной, если  для всех п; иначе говоря,

– ортогональная нормированная система функций, если

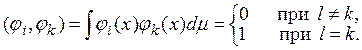
Примеры. 1. Классическим примером ортогональной нормированной системы функций на отрезке  является тригонометрическая система:

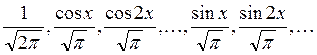
2.         Многочлены

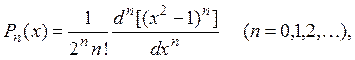
называемые многочленами Лежандра, образуют ортогональную систему функций на отрезке [–1,1]. Нормированную ортогональную систему образуют функции

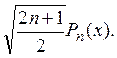
Легко видеть, что ортогональная система функций линейно независима. Действительно, умножая соотношение

на  и интегрируя, получим

и так как  то

Отметим еще, что если в пространстве L₂ существует счетное всюду плотное множество  то любая ортогональная нормированная система функций  не более чем счетна.

Действительно, пусть  тогда

Для каждого  выберем  из нашего всюду плотного множества так, что

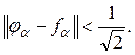
Ясно, что  если  а так как множество всех  счетно, то и самих  не больше, чем счетное множество.

При изучении конечномерных пространств важную роль играет понятие ортогонального нормированного базиса, т. е. ортогональной системы единичных векторов, линейная оболочка которых совпадает со всем пространством. В бесконечномерном случае аналогом такого базиса является полная ортогональная нормированная система функций, т. е. такая система

что

1)

2)

Выше указывались примеры полных ортогональных нормированных систем функций, на отрезках  и [–1,1]. Существование полной ортогональной нормированной системы функций в любом сепарабельном пространстве L₂ вытекает из следующей теоремы:

Теорема. Пусть система функций

                                                        (6)

линейно независима. Тогда существует система функций

                                                       (7)

удовлетворяющая следующим условиям:

1) система (7) ортогональна и нормирована,

2) каждая функция  есть линейная комбинация функций

причем

3) каждая функция f_n есть линейная комбинация функций

причем

Каждая функция системы (2) определяется условиями 1)-3) однозначно (с точностью до знака).

Доказательство. Функция  определяется условиями теоремы однозначно (с точностью до знака). Действительно,

откуда

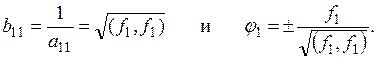
Пусть функции  удовлетворяющие условиям 1)-3), нами уже найдены. Тогда  можно представить в виде

где  при k < n.

Очевидно, что  (предположение  привело бы к противоречию с линейной независимостью системы (6)).

Положим

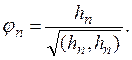
Тогда имеем:

т. е. функция  удовлетворяет условиям теоремы.

Переход от системы (6) к системе (7), удовлетворяющей условиям 1)-3), называется процессом ортогонализации.

Очевидно, что

и, следовательно, системы (6) и (7) одновременно полны или неполны.

Таким образом, в любом вопросе, связанном с аппроксимацией функции f линейными комбинациями функций (6), можно заменить систему (6) ортогональной нормированной системой (7), полученной из (6) процессом ортогонализации.

Как мы уже говорили выше, из существования в L₂ счетного всюду плотного множества вытекает существование счетной полной системы линейно независимых функций. Ортогонализируя ее, мы получим полную счетную ортогональную нормированную систему.

§ 54. Ряды Фурье по ортогональным системам. Теорема Рисса – Фишера

Вводя в n-мерном евклидовом пространстве  ортогональный нормированный базис  можно каждый вектор  записать в виде

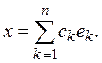                                                              (1)

где