Содержание настоящего параграфа представляет собой, в известном смысле, обобщение разложения (1) на случай бесконечномерного пространства L2.
Пусть
![]() (2)
(2)
– ортогональная нормированная система и ![]()
Поставим следующую задачу: при заданном п подобрать
коэффициенты ![]() так, чтобы расстояние, в смысле
метрики пространства L2, между f и суммой
так, чтобы расстояние, в смысле
метрики пространства L2, между f и суммой
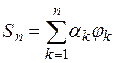 (3)
(3)
было возможно меньше. Положим ![]() Так
как система (2) ортогональна и нормирована, то:
Так
как система (2) ортогональна и нормирована, то:
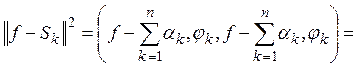
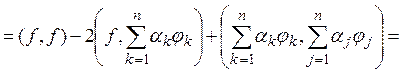
![]()
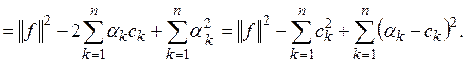 (4)
(4)
Ясно, что минимум этого выражения достигается тогда, когда последнее слагаемое равно нулю, т. е. при
![]() (5)
(5)
В этом случае
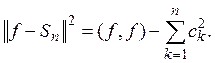 (6)
(6)
Определение. Числа
![]()
называются коэффициентами Фурье функции ![]() по ортогональной системе (2), а ряд
по ортогональной системе (2), а ряд
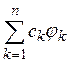
(он может и не быть сходящимся) называется рядом Фурье функции f по системе (2).
Мы показали, что из всех сумм вида (3) при данном п наименее уклоняется от f (в смысле метрики L2) частичная сумма ряда Фурье этой функции. Геометрически этот результат можно пояснить следующим образом.
Функция
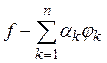
ортогональна всем линейным комбинациям вида
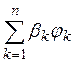
т. е. ортогональна подпространству, порожденному функциями ![]() в том и только том случае, если
выполняется условие (5). (Проверьте это!) Таким образом, полученный нами
результат представляет собой обобщение известной теоремы элементарной геометрии:
длина перпендикуляра, опущенного из данной точки на прямую или на плоскость,
меньше, чем длина любой наклонной, проведенной из той же точки.
в том и только том случае, если
выполняется условие (5). (Проверьте это!) Таким образом, полученный нами
результат представляет собой обобщение известной теоремы элементарной геометрии:
длина перпендикуляра, опущенного из данной точки на прямую или на плоскость,
меньше, чем длина любой наклонной, проведенной из той же точки.
Так как всегда ![]() то из равенства (4)
следует, что
то из равенства (4)
следует, что
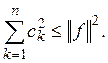
Здесь п произвольно, а правая часть не зависит от п;
следовательно, ряд 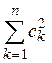 сходится, и
сходится, и
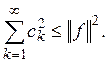
Это неравенство называется неравенством Бесселя.
Введем следующее важное понятие.
Определение. Ортогональная нормированная система (2) называется замкнутой,
если для любой функции ![]() справедливо равенство
справедливо равенство
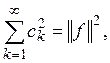 (8)
(8)
называемое равенством Парсеваля.
Из (6) видно, что замкнутость
системы (2) равносильна тому, что частичные суммы ряда Фурье каждой функции ![]() сходятся к f в смысле метрики L2 (т. е. в среднем).
сходятся к f в смысле метрики L2 (т. е. в среднем).
Понятие замкнутости ортогональной нормированной системы тесно связано с введенным в § 53 понятием полноты системы функций.
Теорема 1. В пространстве L2 всякая полная ортогональная нормированная система является замкнутой, и обратно.
Доказательство. Пусть ![]() замкнута; тогда, какова
бы ни была функция
замкнута; тогда, какова
бы ни была функция ![]() последовательность частичных
сумм ее ряда Фурье сходится к ней в среднем. Это означает, что линейные
комбинации элементов системы
последовательность частичных
сумм ее ряда Фурье сходится к ней в среднем. Это означает, что линейные
комбинации элементов системы ![]() всюду плотны в L2, т. е.
всюду плотны в L2, т. е. ![]() полна. Обратно, пусть
полна. Обратно, пусть ![]() полна, т. е. любую функцию
полна, т. е. любую функцию ![]() можно сколь угодно точно аппроксимировать,
в смысле метрики L2, линейной комбинацией
можно сколь угодно точно аппроксимировать,
в смысле метрики L2, линейной комбинацией
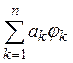
элементов системы ![]() тогда
частичная сумма
тогда
частичная сумма
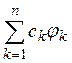
ряда Фурье для f дает, вообще говоря, еще более точную аппроксимацию функции f и, следовательно, ряд
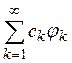
сходится к f в среднем, и равенство Парсеваля имеет место.
В § 53 мы доказали существование полных ортогональных нормированных систем в L2. Поскольку для ортогональных нормированных систем функций из L2 понятия замкнутости и полноты совпадают, существование замкнутых ортогональных систем в L2не нуждается в новом доказательстве, а приведенные в § 53 примеры полных ортогональных нормированных систем являются в то же время примерами замкнутых систем.
Из неравенства Бесселя (7) следует, что для
того, чтобы числа ![]() представляли собой коэффициенты
Фурье некоторой функции
представляли собой коэффициенты
Фурье некоторой функции ![]() по какой-либо ортогональной
нормированной системе, необходимо, чтобы ряд
по какой-либо ортогональной
нормированной системе, необходимо, чтобы ряд
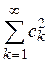
сходился. Оказывается, что это условие не только необходимо, но и достаточно. Именно, справедлива следующая
Теорема 2 (Рисе-Фишер). Пусть ![]() – произвольная ортогональная нормированная система в L2, и пусть числа
– произвольная ортогональная нормированная система в L2, и пусть числа
![]()
таковы, что ряд
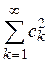
сходится. Тогда существует такая функция ![]() что
что
![]()
и
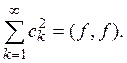
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.