Функции с интегрируемым квадратом, страница 2

сходится почти всюду на R к некоторой функции

                                                        (6)

Итак, мы показали, что если последовательность  фундаментальна в L₂, то в ней найдется подпоследовательность, сходящаяся почти всюду.

б) Покажем теперь, что функция f(x), определяемая равенством (6), принадлежит L₂, и что

                                        (7)

Для любых достаточно больших k и l имеем:

Согласно теореме 3 § 44, в этом неравенстве можно перейти к пределу под знаком интеграла при  Получаем:

откуда следует, что  и  Но из того, что фундаментальная последовательность содержит подпоследовательность, сходящуюся к некоторому пределу, следует, что она сама сходится к тому же пределу[2]. Теорема доказана.

§ 51. Сходимость в среднем. Всюду плотные множества в l₂

Введя в L₂норму, мы тем самым ввели для функций с интегрируемым квадратом некоторое новое понятие сходимости, а именно:

означает, что

Такая сходимость функций называется сходимостью в среднем или, точнее, сходимостью в среднем квадратичном.

Посмотрим, как связано понятие сходимости в среднем с понятием равномерной сходимости, а также с введенным нами в гл. VI понятием сходимости почти всюду.

Теорема 1. Если последовательность {f_n(x)} функций из L₂ сходится равномерно к f(x), то  и {f_n(x)} сходится к f(x) в среднем.

Доказательство. Пусть  Если п достаточно велико, то

откуда

Из этого неравенства сразу вытекают утверждения теоремы.

Из теоремы 1 вытекает, что если любую функцию  можно сколь угодно точно аппроксимировать функциями  в смысле равномерной сходимости, то ими можно аппроксимировать любую функцию из L₂и в смысле сходимости в среднем.

Поэтому любую функцию  можно сколь угодно точно аппроксимировать простыми функциями, принадлежащими L₂.

Покажем, что любую простую функцию а следовательно, и вообще любую функцию из L₂можно сколь угодно точно аппроксимировать простыми функциями, принимающими лишь конечное число различных значений.

Пусть f(x) принимает значения  на множествах  Поскольку суммируема, ряд

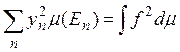
сходится. Выберем число N так, чтобы

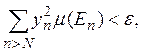
и положим

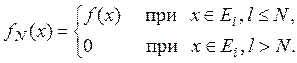
Тогда имеем:

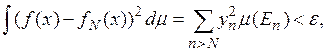
т. е. функции  принимающие конечное число значений, аппроксимируют функцию f с любой точностью.

Пусть R есть метрическое пространство с введенной в нем мерой, удовлетворяющей такому условию (выполненному во всех практически интересных случаях): все открытые и все замкнутые множества в R измеримы, и для любого

                                                        (*)

где нижняя грань берется по всем открытым множествам G, содержащим М. Тогда верна следующая

Теорема 2. Множество всех непрерывных функций всюду плотно в L₂.

Доказательство. В силу сказанного выше, достаточно доказать, что всякая простая функция, принимающая конечное число значений, является пределом, в смысле сходимости в среднем, непрерывных функций. Далее, так как всякая простая функция, принимающая конечное число значений, есть линейная комбинация характеристических функций  измеримых множеств, то достаточно провести доказательство для этих последних. Пусть М – измеримое множество в метрическом пространстве R. Тогда из условия (*) сразу следует, что для любого  найдется замкнутое множество  и открытое множество  такие, что

Определим теперь функцию  положив

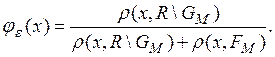
Эта функция равна 0 при  и равна 1 при  Она непрерывна, так как каждая из функций  и непрерывна и их сумма не равна нулю. Функция  не превосходит единицы на  и равна нулю вне этого множества. Следовательно,

откуда и вытекает утверждение теоремы.

Теорема 3. Если последовательность {f_n(x)} сходится к f(x) в среднем, то из нее можно выбрать подпоследовательность  сходящуюся к f(x) почти всюду.

Доказательство. Если последовательность {f_n(x)} сходится в среднем, то она фундаментальна в L₂, поэтому, повторяя рассуждения, проведенные в п. а) доказательства теоремы 4 §50, получаем, что из {f_n(x)} можно выбрать подпоследовательность  сходящуюся почти всюду к некоторой функции  Далее, рассуждения, проведенные в п. б) того же доказательства, показывают, что {f_n(x)} сходится к  также и в среднем, откуда  почти всюду.