Функции с интегрируемым квадратом, страница 7

Доказательство. Положим

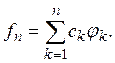
Тогда

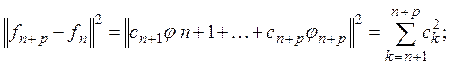
так как ряд (9) сходится, то отсюда вытекает, в силу полноты L₂, сходимость в среднем последовательности  к некоторой функции  Далее,

                                            (10)

причем справа первое слагаемое при  равно  а второе стремится к нулю при  так как

Левая часть равенства (10) от п не зависит; поэтому, переходя в нем к пределу при  получаем, что

Так как, по определению f(x),

то для f выполнено равенство

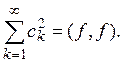
Теорема доказана.

Установим в заключение следующую полезную теорему:

Теорема 3. Для того чтобы ортогональная нормированная система функции (2) была полна, необходимо и достаточно, чтобы в L₂ не существовало такой функции, не эквивалентной  которая была бы ортогональна всем функциям системы (2).

Доказательство. Пусть система (2) полна и, следовательно, замкнута. Если  ортогональна всем функциям системы (2), то все ее коэффициенты Фурье равны нулю. Тогда из равенства Парсеваля получаем:

т.е. f(x) эквивалентна

Обратно, пусть  не полна, т.е. существует такая функция  что

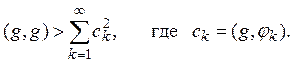
Тогда, на основании теоремы Рисса-Фишера, существует такая функция , что

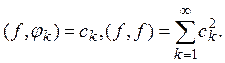
Функция (f – g) ортогональна всем В силу неравенства

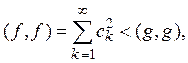
она не может быть эквивалентна  Теорема доказана.

§ 55. Изоморфизм пространств L₂ и l₂

Из теоремы Рисса-Фишера непосредственно вытекает следующая важная

Теорема. Пространство L₂ изоморфно[3] пространству l₂.

Доказательство. Выберем в L₂произвольную полную ортогональную нормированную систему  и поставим в соответствие каждой функции  последовательность  ее коэффициентов Фурье по этой системе. Так как  то  есть некоторый элемент из l₂. Обратно, в силу теоремы Рисса-Фишера всякому элементу  из l₂отвечает некоторая функция f из L₂, имеющая числа  своими коэффициентами Фурье. Установленное соответствие между элементами из L₂и l₂взаимно однозначно. Далее, если

и

то

и

т. е. сумма переходит в сумму, а произведение на число – в произведение соответствующего элемента на это же число. Наконец, из равенства Парсеваля следует, что

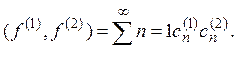                                                  (1)

Действительно, из того, что

и

    вытекает (1). Таким образом, установленное нами соответствие между элементами пространств L₂ и l₂ действительно является изоморфизмом; теорема доказана.

Эта теорема означает, что l₂ можно рассматривать как «координатную запись» пространства L₂. Она позволяет перенести на L₂ факты, установленные ранее для l₂. Например, мы показали в гл. III, ч. I, что всякий линейный функционал в l₂ имеет вид

где у — некоторый элемент из l₂ однозначно определяемый функционалом  Отсюда и из установленного между L₀и l₂ изоморфизма следует, что всякий линейный функционал в L₂имеет вид

где g(x) – некоторая фиксированная функция из L₂. В §24 ч. I было установлено, что  Отсюда и из полученной теоремы вытекает, что

Установленный между L₂и l₂изоморфизм тесно связан с некоторыми вопросами квантовой механики. Первоначально квантовая механика появилась в виде двух внешне различных теорий: «матричной механики» Гейзенберга и «волновой механики» Шредингера. Впоследствии Шредингером была установлена эквивалентность этих двух теорий. С чисто математической точки зрения, различие между этими двумя теориями сводилось к тому, что Гейзенберг использовал в построении соответствующего математического аппарата пространство l₂, а Шредингер — пространство L₂.