Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 9

В качестве целевой функции в данном случае можно выбрать годовую прибыль предприятия, т.е. разницу между доходом от проданной продукции и затратами. Очевидно, лучшим решением будет то, которому соответствует максимальная прибыль.

Составим матрицу решений для данной задачи (табл.2). Значения целевой функции приведены в условных единицах.

Таблица 2                                                                 

Матрица решений для примера 1

Однако анализ альтернатив затруднен наличием внешних факторов, в результате чего в одних условиях (НС) лучше альтернатива х₁, в других (СС) – х₂, в третьих (ВС) – х₃.

Чтобы избавиться от такого рода неопределенности, можно ввести подходящие оценочные (целевые) функции, назначение которых – поставить в соответствие каждой альтернативе только одно число. При этом матрица решений    сведется к одному столбцу, который назовем вектором результатов f_ir: любому варианту х_i приписывается некоторый результат f_ir, являющийся функцией всех последствий этого решения. Другими словами, каждой альтернативе будет соответствовать не строка результатов в матрице, а один результат - f_r(x_i).

Эта функция может иметь разный вид в зависимости от позиции ЛПР. В теории принятия решений различают следующие основные позиции:

- оптимистическую,

- пессимистическую,

- позиции компромисса и

- нейтралитета.

Как же анализировать матрицу решений с этих позиций ЛПР?

Оптимист старается не принимать во внимание плохие результаты, надеясь на наступление наиболее благоприятных внешних условий. Поэтому в качестве компоненты вектора результатов, соответствующей каждому решению, он назначает максимальный результат, т.е. максимальное значение строки:

 - это оптимистическая позиция, или  позиция азартного игрока.

Для пессимиста вполне логично вспомнить закон Мэрфи: “Если несчастье может случиться, оно случится обязательно”. Эта позиция оправдана там, где риск недопустим. Выбирая решение в соответствии с этой позицией, мы гарантируем себе результат, не меньший, чем выбранный. А если повезет, и реализуются более выгодные внешние условия, то можно получить максимальный в данной строке результат. Вектор результатов записывается следующим образом:

 - это пессимистическая позиция.

Позиция компромисса учитывает как максимальный, так и минимальный результаты строки:

Формируя желаемый результат в таком виде, мы исходим из компромисса между оптимистической и пессимистической позициями.

Позиция нейтралитета учитывает все последствия принимаемого решения и поэтому выглядит следующим образом:

.

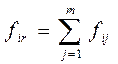2.2 Классические критерии принятия решения

С целью формализации принятия решений в условиях природной неопределенности разработаны классические критерии принятия решений, отражающие ту или иную позиции ЛПР. Рассмотрим классические критерии более подробно.

Минимаксный критерий (ММ), или критерий Вальда

ММ-критерий отражает позицию крайней осторожности, или крайнего пессимизма.

Оценочная функция ММ-критерия:

Оценочная функция  - это результат, соответствующий лучшей альтернативе.

Правило выбора решения в соответствии с ММ-критерием:

Матрица решений  дополняется еще одним столбцом из наименьших результатов f_ir любой строки. Выбрать следует те варианты, в строках которых стоят наибольшие значения f_ir этого столбца.

Выбранные таким образом варианты полностью исключают риск. Т.е. нельзя столкнуться с результатом хуже, чем max f_ir, какие бы условия a_j ни встретились.  Поэтому ММ-критерий считается одним из фундаментальных, в технических задачах он применяется чаще всего.

Однако нежелание рисковать приводит к различным потерям.

Рассмотрим пример 2. Пусть есть две альтернативы (табл.3):

Таблица 3                              

Матрица решений примера 2