Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 12

В этом примере критерий Гурвица предлагает выбрать первую альтернативу, хотя анализ матрицы решений рекомендует использовать точку зрения позиции нейтралитета  и выбрать альтернативу Х₂.

Таким образом, HW используется, если:

- о вероятностях появления событий a_j ничего не известно;

- реализуется малое количество решений;

-  допускается некоторый риск.

Критерий  Гермейера (G)

Этот критерий ориентирован на величины потерь, т. е. на отрицательные значения всех f_ij:

 ,      .

Правило выбора: Матрица решений    дополняется еще одним столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата f_ij на вероятность соответствующего состояния a_j.

Выбираются те варианты, где стоит максимальное значение этого столбца, т. е. критерий G обобщает ММ.

При p_j=1/n,   эти критерии идентичны.

Критерий G применяется, если:

-  вероятности появления a_j известны;

-  результаты f_ij  отрицательны;     

- необходимо считаться с появлением различных событий;

- допускается некоторый риск;

- решения могут реализоваться один или много раз.

Если вероятности p_j известны не очень надежно, а число реализаций мало, то по G-критерию получают неоправданно большой риск.

Мы видим, что при выборе критериев и обосновании позиции имеется свобода для субъективных действий, заключающаяся в выборе позиции ЛПР. Однако, если выбранная альтернатива достаточно устойчива для широкого диапазона позиций ЛПР, то и надежность данного выбора больше.

Если же ситуация неустойчива, т.е. разным позициям ЛПР соответствуют разные альтернативы, то выход один – искать дополнительную информацию о ситуации. Если выбор был сделан в условиях полной неопределенности, то следующий уровень информированности – информация о вероятностях наступления тех или иных внешних условий a_j. Если же известны вероятности, то постановка специальных экспериментов может привести либо к точному знанию, какое именно внешнее условие наступит, либо к косвенным свидетельствам в пользу того или иного условия.

2.5  Планирование эксперимента в условиях неопределенности

Принимая решения в условиях неполной информации, можно  попытаться дополнить имеющуюся информацию путем проведения дополнительных экспериментов.

Когда речь идет о выводах из экспериментов, об их планировании и обработке, мы имеем дело с методами теории статистических решений.

Рассмотрим следующую задачу. Пусть предстоит принять решение в недостаточно выясненных условиях. Имеет ли смысл для уточнения условий в данной неопределенной ситуации предпринять некоторый эксперимент? Естественно, этот вопрос возникает только тогда, когда затраты на эксперимент существенны и сравнимы с тем увеличением выигрыша, которое можно получить, узнав обстановку более точно. Если же затраты на эксперимент пренебрежимо малы, ответ на этот вопрос всегда положителен.

Идеальный эксперимент

Рассмотрим сначала случай “идеального” эксперимента e, приводящего к совершенно точному знанию того состояния α_j, которое имеет место в данной ситуации.

Пусть задана матрица выигрышей f_ij, , , и известны вероятности p(a_j)=p_j.

Обозначим затраты на проведение эксперимента cost.

Сравним средний выигрыш без проведения эксперимента e и средний выигрыш с проведением этого эксперимента.

Без проведения эксперимента e мы имеем средний выигрыш:

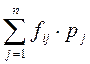                                                                 (1)

Теперь предположим, что провели эксперимент e и выяснили, какое из состояний α_j  является действительным внешним состоянием.

Если это оказалось a₁, то мы должны выбрать стратегию, где достигается .

Здесь b_j - максимальное значение j-го столбца.

И вообще, при a_j выигрыш будет равен максимальному результату в j-ом столбце, т.е. b_j .

Но нужно заранее решить, следует проводить эксперимент или нет. Поэтому выигрыш (абсолютный) =.