Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 16

Рассмотрим случай, когда альтернативы заданы графически (рис.4). Чтобы построить множество Парето, т.е. убрать заведомо худшие альтернативы, сравним различные участки этой кривой. Искомому множеству могут принадлежать только убывающие участки этой кривой, если они не доминируются более правыми участками.

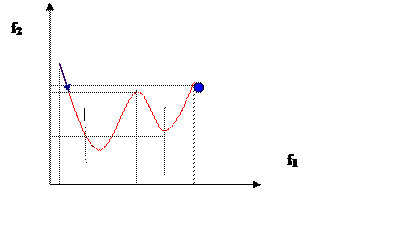
Рис. 4 – Построение множества Парето при графическом задании альтернатив

В результате получим множество Парето, отмеченное на рисунке синим цветом (точка справа и участок кривой со стрелочкой).

Следует заметить, что все альтернативы из множества Парето являются решением многокритериальной задачи в смысле этого принципа, т.е. являются паретооптимальными. Основным недостатком таких решений является их множественность.

3.3 Построение интегрального критерия

Вторым шагом в решении МКЗ является построение некоторого интегрального критерия, позволяющего выбирать наилучшую альтернативу, рассматривая не n критериев (f₁, f₂, ¼ fn), а один – F(x). Этот критерий определяет некоторый компромисс между заданными критериями, и выбранная альтернатива будет оптимальной в смысле этого интегрального критерия. Его роль – поставить в соответствие каждой альтернативе только одно число.

Итак, задача ПР имеет следующий вид

{W, {f_i}_m ,{í,~}}, причем отношения предпочтения и эквивалентности задаются не только на множестве альтернатив, но и на множестве критериев.

Существуют различные методы нахождения компромисса в МКЗ. Рассмотрим подробнее некоторые из них.

Метод арбитражных решений, или метод Нэша

Все альтернативы из множества Парето, будучи несравнимыми,  являются в этом смысле решениями МКЗ, но, как было отмечено ранее, основным недостатком таких решений является их множественность. Поэтому возникает вопрос: а нельзя ли выбрать из них одно, наилучшее в некотором смысле (арбитражное) решение?

Такой метод был предложен Дж. Нэшем, и состоит он в следующем:

Рассмотрим в поле полезности множества Парето антиутопическую точку f⁰, которая имеет координаты {f_i^min}, где - минимально возможная оценка альтернатив по i–му критерию; и рассмотрим произведение разностей координат альтернативы x и точки АУТ. В качестве наилучшей выберем ту, для которой это произведение максимально:

F(x)=.

Пример. Множество Парето состоит из 4 точек (см. рис.5): х₁(2;6), х₂(3;4), х₃(5;2), х₄(6;1). Точка АУТ в поле полезности решений  имеет координаты (2;1).

Найдем значения арбитражного критерия для каждой альтернативы:

для точки 1: F(x₁)=(2-2)(6-1)=0

для точки 2: F(x₂)=(3-2)(4-1)=3

для точки 3: F(x₃)=(5-2)(3-1)=6 ® max для точки 4: F(x₄)=(6-2)(1-1)=0.

Максимальное значение критерия, равное 6, у альтернативы x₃ - она и будет оптимальной с точки зрения критерия Нэша.

       1(2;6)

6         ·  

1          ·                                ·4(6;1)

АУТ (2;1)

2                               6 

 Рис. 5 – К методу Нэша

Замечание: Использование критерия Нэша может быть неэффективным при большом числе критериев.

Использование контрольных показателей

Если множество Парето содержит большое число альтернатив, то ЛПР может искусственно уменьшить границы поля полезности и не рассматривать альтернативы, у которых по отдельным критериям слишком низкие оценки. Для этого вводится система некоторых ограничений.

Пусть задана система нормативных показателей {f_i^*}_n, таких, что f_i (x)³ f_i^*, т.е.  для каждого критерия задана точная нижняя грань, начиная с которой альтернатива может входить в область допустимых решений.

Тогда для каждой критериальной оценки альтернативы х вычислим отношение , т.е. оценим, насколько далеко от допустимой границы находится данная альтернатива по каждому из критериев. Выберем в качестве интегрального критерия минимальное отношение – 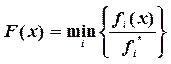 . Наилучшей будет та альтернатива, для которой это отношение максимально:

.

Пример. Для альтернатив из предыдущего примера возьмем следующие контрольные показатели (ограничения): f₁^*=3; f₂^*=2. Тогда поле полезности решений изменится (пунктирные линии на рис.6), уменьшится и количество альтернатив - уйдут точки 1 и 4. Для оставшихся альтернатив построим интегральную оценку: