Найдем сначала оптимальную стратегию Р. Она должна обеспечить выигрыш, не меньший ν при любой стратегии противника, и = ν приего оптимальном поведении Q. Пусть ν>0. Чтобыэто выполнялось,достаточно, чтобы все элементы матрицы aij >0. В противном случае можно прибавить ко всем элементам матрицы А достаточно большое число М, тогда цена игры увеличится на М, а вероятности останутся теми же.
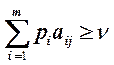 для любого j. Введем
обозначения: xi=pi/ν, тогда
для любого j. Введем
обозначения: xi=pi/ν, тогда
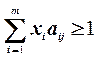 ,
,  , выбор должен быть максимально возможным,
следовательно, 1/ν принимает минимальное значение. Таким образом,
, выбор должен быть максимально возможным,
следовательно, 1/ν принимает минимальное значение. Таким образом, 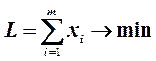 .
.
Найдем теперь оптимальную стратегию 2-го игрока. Все аналогично решению игры для первого игрока, только второй игрок стремится не максимизировать, а минимизировать свой проигрыш ν, а значит, максимизировать величину 1/ν.
Поскольку стремление к цене игры ν выгодно 2-му игроку, то он проиграет не больше ν при любой стратегии 1-го игрока.
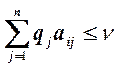 для любого i. Заменим yj=qj/ν,
тогда
для любого i. Заменим yj=qj/ν,
тогда
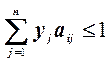 , а т.к. Σqj=1,
то Σyj=1/ν. Требуется так выбрать переменные yj,
чтобы максимизировать функцию
, а т.к. Σqj=1,
то Σyj=1/ν. Требуется так выбрать переменные yj,
чтобы максимизировать функцию 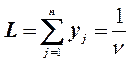 , или, что то же самое,
минимизировать функцию L’=-L:
, или, что то же самое,
минимизировать функцию L’=-L: 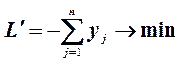 .
.
4.7 Симметричные игры
Рассмотрим один частный класс игр.
Опр. Квадратная матрица А={aij}называется кососимметричной, если aij=-aji для любого i.
Th. Значение симметричной игры равно нулю. Кроме того, если х – оптимальная стратегия первого игрока, то х также оптимальная стратегия для второго.
Пример.
|
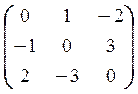
По теореме n=0; а т.к. P=Q, то найдем P.
Средний выигрыш 1-го игрока при любой стратегии 2-го
![]() -р2+2р3=0
→ р2=2р3
-р2+2р3=0
→ р2=2р3
р1 -3р3=0 → р1 =3р3
-2р1+3р2 =0
р1+ р2+ р3=1
2р3 +3р3 +р3=1
6р3=1; р3=1/6; р2=1/3; р1=1/2
P=Q=(1/2; 1/3; 1/6)
Если выполнено хотя бы одно из следующих условий:
- не всегда выигрыши игроков противоположны, т.е. f1=-f2;
- интересы сторон даже с двумя участниками не обязательно противоположны,
существует хотя бы одна ситуация, когда интересы игроков близки;
- различие в оценках ситуации оставляет место для соглашений, договоров и кооперации;
- для ЛПР цена игры имеет незначительную ценность, ,он готов на использование дополнительных стратегических возможностей, чтобы получить больше, чем гарантированный результат, - следует перейти к другой форме игры – биматричной.
Биматричная игра – это конечная игра двух лиц с ненулевой суммой
Выигрыши игроков определяются следующими матрицами:
А=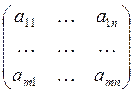 - матрица выигрышей первого игрока, или ||аij||,
- матрица выигрышей первого игрока, или ||аij||,
В=||bij|| - матрица выигрышей второго игрока.
Решение игры будем искать, ориентируясь на следующую логику. С точки зрения первого игрока его средний выигрыш (матрица А) должен быть больше или равен среднему выигрышу второго игрока при любой стратегии 2-го.
Средний выигрыш первого игрока: Мn1=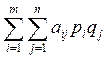 ,
,
Средний выигрыш второго игрока: Мn2= ,
,
å bij pi £ å bij pi qj , å pi=1
å aij qj £ å aij pi qj , å qj=1, для любых i, j.
В случае, когда матрицы выигрышей имеют размерность 2х2, биматричную игру можно свести к решению двух матричных.
Пример. Заданы две
матрицы игры: А=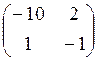 , В=
, В=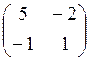
p1=  =
=![]() =
=![]() ; p2=
; p2=  =
=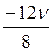 =
=![]() Þ
Þ 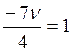 Þ n=
Þ n=![]()
р1=![]() ;
р2=
;
р2=![]()
Матрица В решается с точки зрения первого игрока, т.к. целью второго является также выиграть как можно больше:
q1=  =
=![]() ; q2=
; q2=  =
=![]() Þ
Þ  Þ n=
Þ n=![]() ;
q1=
;
q1=![]() ; q2=
; q2=![]()
Ответ: Р=(![]() ;
;![]() ); n1=
); n1=![]() ; Q=(
; Q=(![]() ;
;![]() ); n2=
); n2=![]() .
.
Это решение выгодно обоим игрокам, т.к. их гарантированные результаты: (-1) – для первого и (-1) – для второго.
Литература
2. Мушик Э., Мюллер П. Методы принятия технических решений. М.: Мир.-1990.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.