Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 17

  

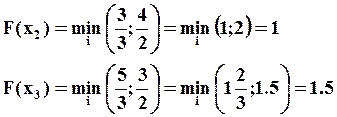
Наилучшей в смысле критерия контрольных показателей будет третья альтернатива.

Следует заметить, что данный метод нельзя применять, если среди оценок есть отрицательные или среди ограничений – нулевые значения. Поскольку для принятия решения важно относительное расположение альтернатив, а не их абсолютные оценки, то это замечание можно обойти следующим образом: сдвинуть те оси, где есть отрицательные оценки, на величину │М+1│, где │М│ - максимальное по модулю значение отрицательной оценки по данному критерию. Однако такое преобразование изменит  координаты утопической и антиутопической точек, что необходимо учесть при использовании других методов.

f₂         1(2;6)

6         ·  

1          ·                                ·4(6;1)

АУТ (2;1)f₁                 

2                               6 

 Рис. 6 – К методу контрольных показателей

Простейший метод

Пусть, как и в предыдущем случае, задана система контрольных показателей {f_i^*} таких, что f_i³f_i^*. И пусть среди заданных критериев можно выбрать один – главный – критерий, назовем его f₁ – главный критерий. Тогда МКЗ сводится к однокритериальной задаче    f₁(x)®max_х  при ограничениях   f_i (x)³f_i^*.

Вернемся к последнему примеру. В поле полезности, ограниченном контрольными показателями, осталось две альтернативы – 2 и 3. Если в качестве главного выбрать первый критерий, то наилучшей будет альтернатива 3, если главный второй критерий, то наилучшая альтернатива – вторая  (рис. 6).

Введение метрики в пространстве целевых функций

Как известно, самой лучшей точкой в критериальном пространстве является точка УТ – утопическая точка с координатами {f_i^max}, где  – решения n однокритериальных задач. Чем ближе рассматриваемая альтернатива к УТ, тем она лучше.

Введем понятие расстояния  h(x) от альтернативы х до УТ:

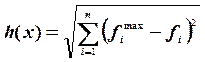, тогда наилучшей альтернативой будет та, расстояние от которой до точки УТ  наименьшее:

.

В данном случае роль интегрального критерия играет расстояние от рассматриваемой альтернативы до утопической точки.

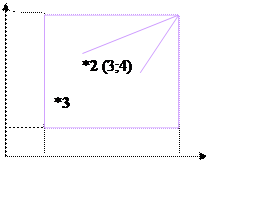
Вернемся опять к примеру (рис.7). Расстояние h(x) определяет длину прямой, соединяющей альтернативу х с УТ.

f₂           1(2;6)

6         ·                                 · УТ (6;6)

1          ·                                ·4(6;1)

АУТ (2;1)

2                               6      f₁

Рис. 7 – Введение метрики

Посчитаем  расстояния для каждой альтернативы:

h(x₁)==4,

h(x₂)==,

h(x₃)=Ö(6-5)²+(6-3)²=,

h(x₄)==5.

Минимальное расстояние  – для третьей альтернативы, она и будет наилучшей с точки зрения используемого интегрального критерия.

Данный метод практически не имеет ограничений в применении, не требует преобразования координат и может использоваться в задачах произвольной размерности.

3.3.5  Свертка

Мы рассмотрели ситуации, в которых все критерии были одинаково важными. При решении практических задач ЛПР, как правило, ранжирует критерии в соответствии со своими предпочтениями. В этом случае в качестве интегрального критерия используются различные виды сверток

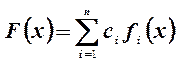,       – линейная свертка, здесь x – альтернатива из множества W;

f_i (x) – оценка альтернативы x по i-му критерию;

с_i – весовые коэффициенты, с которыми оценки альтернатив входят в интегральный критерий. с_i  – коэффициенты значимости, или коэффициенты относительной важности критериев.

Коэффициенты с_i можно найти, например, из специально организованной экспертизы: m экспертов должны расставить (ранжировать) критерии по важности:ранг 1 присвоить самому важному критерию и т.д. Пусть r_ij – ранг, который присвоил j-ый экперт i-му критерию. Чтобы получить числовую оценку, введем новый коэффициент

.

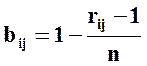Тогда коэффициент значимости i-го критерия с точки зрения j-го эксперта:

.

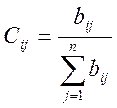Обобщенные коэффициенты получим, усреднив оценки экспертов.

Пусть g_j – компетентность j-го эксперта, тогда

.

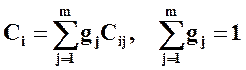Еще один метод назначения коэффициентов относительной важности основан на внесении предпочтений во множество критериев. Он состоит в следующем.