Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 10

Х₁    вроде бы более выгодная, однако согласно ММ оптимальной считается Х₂.

Потери будут еще больше, если:

1) a₂  реализуется чаще, чем a₁, и

2) решение реализуется многократно, - т.е. в многочисленных практических ситуациях пессимизм ММ-критерия может оказаться очень невыгодным.

Применение ММ-критерия оправдано, если:

- о возможности появления внешних состояний a_j ничего не известно;

- приходится считаться с появлением различных внешних состояний a_j;

- решение реализуется один раз;

- необходимо исключить какой бы то ни было риск.

Критерий   Сэвиджа (S)

Это критерий относительного пессимизма, который оперирует понятием риска, или остатка:

    - разница между максимальным значением j-го столбца и результатом в данном столбце, соответствующим i-ой альтернативе. В столбец вектора результатов записывается максимальное значение риска для каждой альтернативы:  

Оценочная  функция выбирается как минимальное значение риска среди всех альтернатив

Здесь    трактуется как максимальный дополнительный выигрыш, который достигается, если в состоянии  a_j  вместо варианта х_i выбрать другой, оптимальный для этого внешнего состояния, вариант. Или как потери от замены оптимального для  a_j состояния варианта на вариант х_i. Затем эти максимально возможные потери минимизируются.

Правило выбора: Любой элемент матрицы решений    вычитается из наибольшего результата    соответствующего столбца. Разности D_ij образуют матрицу остатков . Эта матрица дополняется столбцом наибольших разностей  . Выбирается вариант, где стоит наименьшее для этого столбца значение.

Требования к применению S-критерия те же, что и для ММ.

Вернемся к примеру 1. Дополним матрицурешений столбцами для векторов результатов.

Таблица 4                                                      

Выбор оптимальной альтернативы в примере 1

Для ММ-критерия выбираем из каждой строки минимальное значение результата. Лучшая альтернатива – х₁, ей соответствует максимальное значение компоненты вектора результатов.

Для применения критерия Сэвиджа надо построить матрицу рисков, или остатков.

Для этого из мксимального результата каждого столбца вычтем соответствующее значение результата из матрицы решений. В вектор результатов матрицы остатков выносится максимальное значение строки. Лучшей альтернативе соответствует минимальное значение максимального риска, связанного с каждой альтернативой.

Таблица 5                                                      

Матрица остатков в примере 1

С точки зрения критерия Сэвиджа лучшая альтернатива – х₂, ей соответствует минимальный риск.

Критерий  Байеса-Лапласа (BL)

Все рассмотренные выше критерии используются в условиях полной неопределенности, т.е. в условиях, когда ничего не известно о вероятностях наступления внешних событий. Как правило, если в этих условиях выбор затруднен, ЛПР ничего не остается, как искать дополнительную информацию. Такой дополнительной информацией может быть, например, информация о вероятности аналогичных исходов в прошлом или оцененная по результатам экспертных опросов возможность наступления того или иного внешнего события. Главное, чтобы рассматриваемые события составляли полную группу.

Пусть p_j -  вероятность появления внешнего состояния a_j, .

В отличие от рассмотренных ранее критериев критерий BL учитывает все возможные последствия каждой альтернативы.

Тогда для BL-критерия:

       и      , т.е.

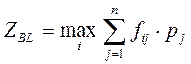
Правило выбора: Матрица решений  дополняется еще одним столбцом, содержащим математические ожидания результатов каждой строки. Выбираются те варианты х_i,  в строках которых стоит наибольшее значение  f_ir этого столбца.