Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 18

Пусть удается количественно выразить отношения предпочтения между критериями: критерий f_i предпочтительнее критерия f_j в h раз: . Тогда коэффициенты относительной важности этих критериев связаны между собой линейным уравнением C_i=hC_j. Это следует из теоремы:

Th. Если , то C_i=hC_j, C_i>0, åC_i=1. 

Решая систему линейных уравнений, получим искомые коэффициенты.

Пример. Пусть варианты некоторой системы оцениваются по четырем критериям с пятибалльной шкалой. Значения критериевf_i(х) даны в табл.13.

Пусть известно, что ,   f₂~ f₃ , .

Решение. Составим систему линейных уравнений для определения коэффициентов C_i:

C₁=1,5C₂;  C₂=C₃;   C₃=C₄;   C₁+C₂+C₃+C₄=1;

Отсюда следует, что C₁=3/8; C₂=2/8; C₃=2/8; C₄=1/8.

В табл. 13 приведены значения интегрального критерия «Линейная свертка».

Таблица 13                                     

Оценки вариантов по критериям                                                                  

По этому критерию лучшая альтернатива – Х₂.

Задачи, в которых выполняются условия для использования линейной свертки, часто встречаются в практике. Это задачи, связанные с критериями суммарного ущерба или прибыли, дохода, денежных или временных затрат по годам планирования или по этапам жизненного цикла экономических информационных систем и т. п., т.е. там, где допускается, что низкая ценность одной частной характеристики результата  компенсируется высокой ценностью другой.

Свертка может быть не только линейной, но и квадратичной:

,

сверткой порядка t:

,

Величина t, стоящая в показателе степени, отражает допустимую степень компенсации малых значений одних равноценных критериев большими значениями других. Чем больше значение t, тем больше степень возможной компенсации.

Например, при , т.е. когда недопустима никакая компенсация и требуется выравнивание значений всех критериев (равномерное «подтягивание» значение всех критериев к их наилучшему уровню), интегральный критерий приобретает вид

.

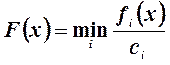Если t→0, т.е. требуется обеспечение примерно одинаковых уровней значений отдельных частных критериев, то интегральный критерий имеет вид

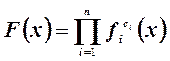 – мультипликативная функция.

При t=1 имеем линейную свертку, приt=2 – квадратичную.

В задачах планирования ударов «по узкому месту» допустима компенсация увеличения одного из критериев сколь угодно большим уменьшением остальных, т.е. , тогда интегральный критерий можно использовать в виде

.

Используя в качестве интегрального критерия свертку, выбирают в качестве лучшей ту альтернативу, для которой F(x) имеет максимальное значение.

Замечание. Входящие в интегральный критерий целевые функции имеют разную размерность и выражены в разных шкалах. Поэтому необходимо предварительно выразить все оценки в одной однородной шкале. Целесообразно использовать для этого  следующий прием

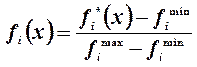, где f_i^*(x) – оценка альтернативы x по i-му критерию в «родной» шкале, f_i^max иf_i^min – максимальное и минимальное значения альтернатив по  i-му критерию. Полученные оценки принадлежат отрезку [0;1] и являются дробными, что не всегда удобно для расчетов. Поэтому можно, умножив все оценки по соответствующим критериям на наименьшее общее кратное, перейти в целочисленную шкалу. Сдвиг по шкале на общую для каждого из критериев величину позволит избавиться от отрицательных оценок.

3.4  Метод многокритериальной полезности альтернатив

(Multi-Attribute Utility Theory – MAUT)

Используется при возможном структурировании системы целей, представлении ее в виде иерархии.

Идея – оценить полезность каждой альтернативы с точки зрения достижения глобальной цели.