Аналогично P(B3)=0.20 (ср. выигрыш равен 5.20).
Поскольку Р(Вk)=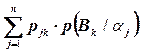 , то для k=1 получим Р(В1)=0,46, для k=2 Р(В2)=0,34, для k=3 Р(В3)=0,20. Полный средний выигрыш
будет равен
, то для k=1 получим Р(В1)=0,46, для k=2 Р(В2)=0,34, для k=3 Р(В3)=0,20. Полный средний выигрыш
будет равен 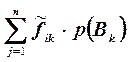 , т.е.
, т.е.![]() , а был
до проведения эксперимента равен 5.2, т.е. средний выигрыш увеличился на 0.145.
, а был
до проведения эксперимента равен 5.2, т.е. средний выигрыш увеличился на 0.145.
Отсюда, если cost<0.145, то эксперимент e целесообразен, если же cost³0.145, то нет. В этом случае следует выбрать альтернативу, оптимальную по BL-критерию.
Контрольные вопросы
17. Понятие рационального выбора.
18. Основные типы неопределенностей, встречающихся при принятии решений.
19. Характеристика неопределенностей природы.
20. В чем состоит идея преодоления природных неопределенностей?
21. Роль вектора результатов.
22. В чем проявляется субъективизм при принятии решения?
23. Сколько целевых функций может быть в задачах неопределенности природы?
24. Как направлены целевые функции в задачах неопределенности природы?
25. Как сравнивать альтернативы в задачах неопределенности природы?
26. Какая позиция ЛПР не допускает риск?
27. Что является формой представления задачи неопределенности природы?
28. Какой смысл имеют числа в матрице решений?
29. Позиция ЛПР и классические критерии.
30. Какие критерии выражают пессимистическую позицию ЛПР?
31. Смысл и роль оценочной функции.
32. Понятие риска.
33. Какой знак имеют элементы матрицы остатков?
34. Какие критерии применяются в условиях полной неопределенности?
35. Какой критерий применяется в условиях риска, когда известны вероятности внешних условий?
36. Какой критерий работает с матрицей остатков?
37. Когда имеет смысл для уточнения условий в данной неопределенной ситуации предпринять некоторый эксперимент?
38. Как вычислить допустимую стоимость эксперимента?
39. Как оценить целесообразность эксперимента?
40. Дать определение теоремы Байеса.
41. В чем состоит идеальный эксперимент?
42. Что называют неидеальным экспериментом?
3 Принятие решения при неопределенности целей
3.1 Постановка многокритериальной задачи
В случае многокритериальной постановки задача принятия решения имеет следующий вид:
(W, {fi}n, {ý,~}), где {fi}n - n целевых функций fi, каждая из которых сформулирована в виде fi(х)®max; ý - отношение предпочтения; ~ - отношение эквивалентности.
Однако не любая задача принятия решения является многокритериальной, т.к. цели могут находиться друг с другом в различных отношениях:
1) цели могут быть взаимно нейтральны – в этом случае задача по отношению к отдельным целям рассматривается независимо;
2) цели кооперируются, тогда достижение одной цели одновременно приводит к достижению других;
3) цели конкурируют – одной цели можно достичь только за счет другой.
В первом случае задача может быть решена, например, таким способом.
Критерии ранжируются по важности: самому значимому присваивается ранг, равный 1, следующему по важности - ранг 2 и т.д. Из исходного множества альтернатив выбираются альтернативы, удовлетворяющие цели первого ранга
![]() , xЄΩ; при этом альтернативы, оценки
которых по первому критерию можно считать достаточно высокими, образуют
множество Ω1.
, xЄΩ; при этом альтернативы, оценки
которых по первому критерию можно считать достаточно высокими, образуют
множество Ω1.
Затем из вновь полученного множества Ω1 отбираются альтернативы, наилучшие с точки зрения критерия второго ранга
![]() и т.д.
и т.д.
Может оказаться, что после последней оптимизационной процедуры останется несколько альтернатив. Но, поскольку все они эквивалентны с точки зрения наименее значимого критерия, то ЛПР может выбрать любую из них.
Во втором случае задача также решается как однокритериальная для одной из кооперирующихся целей - остальные в этом случае достигаются одновременно.
И только в третьем случае мы имеем действительно многокритериальную задачу (МКЗ), решить которую можно, только найдя определенный компромисс между критериями.
Таким образом, механизм ситуации «Неопределенность целей» состоит в том, что трудно осуществить выбор, когда одни альтернативы лучше по одним критериям, другие – по другим. Задача состоит в том, чтобы разрешить эту неопределенность и найти лучшее по совокупности критериев решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.