Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 26

y1  y2  y3

Пример 1. Пусть платежная матрица задана в виде

 

, тогда первый игрок выбирает 1-ую стратегию, ориентируясь на максимальный выигрыш 5. Второй игрок выбирает свою вторую стратегию, чтобы проиграть 1, а не 5. На следующем шаге 1-ый игрок ходит своей второй стратегией, чтобы максимизировать свой выигрыш при 2-ой стратегии 2-го игрока, на что тот отвечает опять же своей второй стратегией, чтобы минимизировать свой проигрыш. Далее игра становится устойчивой, т.к. ситуация (x₂,y₂) выгодна обоим игрокам.

Когда в игре есть ситуация равновесия, то через какое-то число ходов игра сойдется и станет устойчивой – игрокам нет смысла скрывать свои стратегии. Если игра не имеет ситуации равновесия, то игроки сохраняют свои стратегии в тайне.

Чтобы определять ситуации равновесия, надо научиться находить гарантирующие стратегии для каждого из игроков.

Вернемся к Примеру 1. Анализируя матрицу игры, I игрок должен выбрать для каждой своей стратегии тот гарантированный результат, который он получит независимо от того, какую стратегию применит II игрок. Очевидно, этот результат равен    . Тогда из всех стратегий он должен выбрать ту, для которой этот минимум максимален:

.

Здесь n₁ – гарантированный результат для I игрока: он не получит меньше, чем  n₁, при любой стратегии II игрока. Следует заметить, что аналогичного принципа придерживается ЛПР в нестратегической игре с природой, когда, не желая рисковать, он выбирает минимаксный критерий.

Аналогично, II игрок выбирает для каждой своей стратегии максимальный проигрыш, а затем из всех стратегий выбирает ту, для которой этот максимальный проигрыш является минимальным:  

.

Здесь n₂ – гарантированный результат для II игрока: он не проиграет больше, чем n₂, при любой стратегии первого игрока.

Соответствующие стратегии носят названия:  максиминная - для I игрока, - и минимаксная – для второго.

Гарантированные результаты: n₁=n – нижняя цена игры, n₂= – верхняя цена игры.

Можно показать, что всегда n£, или

£.

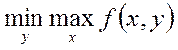Действительно, £ - по свойству с.р. Но если f(x)<g(x), minf(x)<ming(x), т.е. £, справа стоит константа. Если функция ограничена сверху константой, то и максимум этой функции ограничен ею же. Т.е. £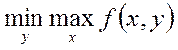, ч.т.д.

Это неравенство носит название неравенство  минимаксов и успешно используется для решения игр.

Если n=, то это ситуация равновесия, или седловая точка. Соответствующая пара стратегий является решением игры.

Пример.  Пусть задана матрица игры:                   

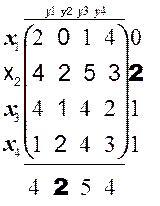
Найдем гарантированные результаты каждого игрока:

=max_xmin_yf_ij=2; =min_ymax_xf_ij=2 – в игре есть седловая точка. Тогда цена игры равна 2, а решение игры – (х₂, y₂).

Седловых точек в игре может быть несколько, причем цена игры в каждой одинакова.

Стремление игроков к ситуации равновесия, описываемой седловой точкой, носит название принципа достижимости целей, т.к. только ситуации равновесия могут быть предметом договоров, которые будут соблюдаться (игрокам невыгодно отступать от такой ситуации).

К сожалению, далеко не все игры имеют седловые точки, они скорее исключение, чем правило. Обычно гарантированные результаты игроков не совпадают. Как же решать игру в этом случае? Существуют ли оптимальные решения в играх без седловых точек?

Теорема Неймана гарантирует, что каждая антагонистическая игра имеет оптимальные стратегии.

Пример 2. Задана матрица игры:     = 4; =6.

Если первый игрок будет придерживаться своей оптимальной стратегии (х₂), то его выигрыш будет не меньше, чем 4. Второй игрок, придерживаясь своей гарантирующей стратегии y₁, проиграет не больше, чем 6.  Анализируя поведение игроков при выборе хода, можно сообразить, что пока твои ходы знает противник, ситуации равновесия не будет. В играх без седловой точки свои ходы надо тщательно скрывать. Это игры с закрытой информацией. Однако интервал [4;6] каждый из игроков хочет перераспределить в свою пользу, и это выгодно им обоим. Значит, надо придумать такую процедуру поведения, чтобы nÎ[4;6].  Правильное поведение состоит в том, чтобы стратегию выбирать случайно – не на основании каких-то разумных соображений, - но сама схема рандомизации должна выбираться разумно. В этом состоит идея использования смешанных стратегий.