Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 27

Смешанная стратегия – это случайная величина, значениями которой являются чистые стратегии игрока. Это сложная стратегия, состоящая в случайном чередовании двух или более чистых стратегий с определенными частотами.

В теории игр доказано, что устойчивое решение в играх без седловой точки лежит в области смешанных стратегий.

Тогда смешанная стратегия первого игрока – это случайная величина

x = 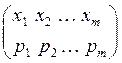, или просто вероятностное распределение на множестве чистых стратегий Р = (р₁, р₂, ¼, р_m), причем .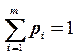

Смешанная стратегия второго игрока – это случайная величина

h = 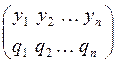, Q = (q₁, q₂, ¼, q_n), .

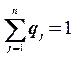При использовании смешанной стратегии перед каждой партией игры пускается в ход какой-то механизм случайного выбора, обеспечивающий появление каждой стратегии с некоторой частотой, затем берется та стратегия, на которую пал жребий. Применение смешанной стратегии - это гибкая тактика, при которой противник не знает и не может знать заранее, с чем ему придется встретиться.

Очевидно, что любая чистая стратегия является частным случаем смешанной: например, х₁=Р(1,0,…,0). Таким образом, для любой игры существует пара (P,Q) смешанных стратегий. Платеж, соответствующий паре (P,Q), называется ценой игры n. Поскольку первый игрок гарантирует себе при этом выигрыш n³, а второй игрок гарантирует себе проигрыш n£, то применение смешанных стратегий выгодно обоим игрокам.

Некоторые чистые стратегии могут не войти в P или Q. Их частоты тогда будут равны нулю. В этом случае стратегии, которые входят в оптимальную смешанную стратегию (им соответствуют ненулевые вероятности), называются активными стратегиями.

Решить игру – значит найти цену игры и оптимальные стратегии каждого игрока.

Таким образом, можно выделить следующий алгоритм решения игры.

1. Упростить игру.
2. Найти гарантированные результаты для каждого игрока.
3. Если существует седловая точка, то найти решение игры в чистых стратегиях.
4. Если седловой точки нет, то найти решение игры в смешанных стратегиях.

Рассмотрим по очереди каждый из этапов.

Упрощение игры

Решение игры mхn – довольно трудоемкая задача, особенно если у нее нет седловой точки. Дальше мы увидим, что матричную игру произвольной размерности можно свести к задаче линейного программирования. Однако игры небольшой размерности можно решить аналитически. Это относится к играм, где хотя бы у одного игрока имеется только две стратегии. Поэтому упрощение игр – необходимая составляющая процесса решения.

Игру иногда удается упростить, если уменьшить в ней число стратегий путем вычеркивания некоторых лишних стратегий. Лишние стратегии – это

1)  дублирующие

2)  заведомо невыгодные.

Пример 3. Пусть задана матрица игры

Проанализируем строки этой матрицы, т.е. стратегии первого игрока. В этой матрице х₁=х₃ – дублирующие стратегии, оставим одну, например, х₁. Далее, при любой стратегии второго игрока (индекс j)   f_2j£f_1j: стратегия х₁ предпочтительнее стратегии х₂, последнюю можно вычеркнуть.

Получилась матрица

Встанем теперь на точку зрения второго игрока и проанализируем столбцы. При любой стратегии первого игрока f_i4£f_i3 – проигрыш второго игрока в случае y₄ меньше, чем для y₃. Значит, стратегия y₃ – заведомо невыгодная, ее можно убрать. Следовательно, окончательный вид матрицы

От матрицы 4х4 мы пришли к матрице 2х3.В этой игре =1,  =3 – седловой точки нет. Решение игры надо искать в смешанных стратегиях.