Чтобы найти оптимальные стратегии второго игрока, оставим в первоначальной матрице только те стратегии второго игрока, которые образуют точку пересечения (p1,n). Остальные стратегии II игрока будут неактивными, т.к. значения среднего проигрыша в точке р1 для других стратегий (прямые ni) лежат выше. Полученную матрицу 2х2 решим любым удобным способом и найдем вероятности (q1,q2). Рассмотрим пример.
Пример. Решить игру: А=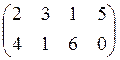 .
.
В этой игре ![]() =1,
=1, ![]() =3. Будем решать ее с точки зрения I игрока.
=3. Будем решать ее с точки зрения I игрока.
![]() n1=2р1+4р2=2р1+4(1-р1)=4-2р1
n1=2р1+4р2=2р1+4(1-р1)=4-2р1
n2=3р1+р2=1+2р1
n3= р1+6р2=6-5р1
n4=5р1+0р2=5р1
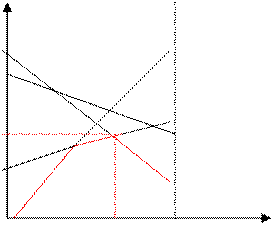
На рис.3.1 изображены графики линейных функций ni. Их область определения – интервал (0,1). Следуя процедуре, отметим нижнюю границу семейства прямых (выделена красным цветом).
 n
n
6 n4
4
n n2
n1
n3
0 р*1 1 р1
Рис. 3.1. Средний выигрыш I игрока.
Верхняя точка границы образована пересечением прямых n3 и n2 , т.е. (р*1, n)În3 Çn2. Координаты точки пересечения найдем из равенства 1+2р1=6-5р1,
Отсюда
7р1=5 и р*1=![]() , р2=
, р2=![]() Þ n=1+ 2*
Þ n=1+ 2*![]() =
=![]() .
.
Для 2-го игрока стратегии y1 и y4 – неактивные, т.к. не используются в смешанной стратегии. Тогда смешанную стратегию второго игрока найдем из
q1= 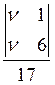 =
=![]() =
=![]() Þ Q= (0;
Þ Q= (0;![]() ;
;![]() ;0).
;0).
Ответ: P=(5/7;2/7), n=17/7; Q=(0;5/7;2/7;0).
Рассмотрим игру m´2 – у 1-го игрока m стратегий, у 2-го игрока – 2 стратегии.
Решаем с точки зрения того игрока, который имеет 2 стратегии – с точки зрения второго.
Р= (р1,¼, рm) – смешанная стратегия 1-го игрока
Q= (q1, q2) – смешанная стратегия 2-го игрока
|
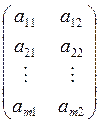 .
.
Средний проигрыш 2-го игрока:
![]() n1= a11 q1+a12 q2=a11+(a11-a12)q1;
n1= a11 q1+a12 q2=a11+(a11-a12)q1;
…
nm= am1 q1+am2 q2=am1+(am1-am2)q1.
Решаем, как и в первом случае, графически. Гарантированный результат второго игрока
![]() .
.
Поэтому в семействе прямых, описывающих средний проигрыш 2 игрока, отмечаем верхнюю границу и выбираем на ней самую нижнюю точку. Ее координаты определяют искомую вероятность q1 и цену игры n. Тогда активными стратегиями первого игрока будут те, которые соответствуют прямым, образующим точку пересечения (q1,n). Оптимальные стратегии первого игрока определим из матрицы 2х2.
Пример.
Решить матрицу игры: А=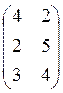
Средний проигрыш второго игрока зависит от вероятности q1:
n1=4q1+2q2=4q1+2(1-q1)=2+2q1 - при первой стратегии 1 игрока,
n2=2q1+5q2=5-3q1 - при второй стратегии 1 игрока,
 n3=3q1+4q2=4-q1 - при третьей
стратегии 1 игрока.
n3=3q1+4q2=4-q1 - при третьей
стратегии 1 игрока.
5
4 n1
n n3
2 n2
0 q*1 1 q1
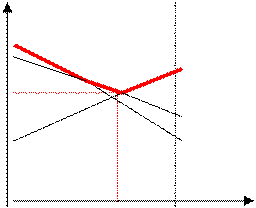
Рис. Графическое решение игры
Верхняя граница семейства прямых выделена жирной линией. Искомая точка образована пересечением прямых n1 и n3: (q*1, n) Î n1 Çn3 Þ 2+2q1=4-q1, 3q1=2.
q*1=![]() , q2=
, q2=![]() Þ n=2+ 2*
Þ n=2+ 2*![]() =
=![]() .
.
Оптимальную стратегию первого игрока найдем изматрицы A= :
:
AT= 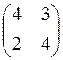 Þ p1=
Þ p1= 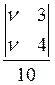 =
=![]() =
=![]() Þ P= (
Þ P= (![]() ; 0;
; 0; ![]() ).
).
Ответ: Q=(2/3; 1/3), n=10/3, P=(1/3; 0; 2/3).
Смешанная стратегия игрока в разных случаях имеет разный смысл. Иногда конфликт должен быть разрешен всего за один ход противников. Например, решение строить в регионе крупное производство или размещение заказа на разных предприятиях, или установление цены на продукцию, или оснащение производства современным оборудованием, или ведение боевых действий с применением разных стратегий и т.д.
Далеко не всегда игры имеют размерность, допускающую аналитическое решение. Как правило, размерность задачи больше 2-х.
В этом случае решение игр возможно путем сведение ее к задаче линейного программирования.
4.7 Решение игр mxn
Пусть необходимо найти смешанные стратегии: 1-го игрока Р=(р1, р2, …, рm) и 2-го игрока - Q=(q1, q2, …, qn), причем Σpi=1, Σqj=1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.