Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 13

С учетом стоимости эксперимента (которую надо вычесть из выигрыша) средний выигрыш с проведением идеального эксперимента e равен

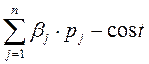                                                                     (2)

Итак, мы должны проводить эксперимент, если величина (2) больше, чем (1), иначе эксперимент не нужен, т.е.

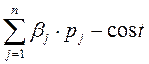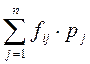>.                                                          (3)

Проведем некоторые преобразования. Перепишем неравенство (3) в другом виде:

сost< для любого i, или    сost<.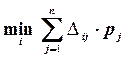

Другими словами, эксперимент e нужно проводить, если затраты на его проведение меньше минимального среднего риска

                                                  сost<.

В противном случае следует воздержаться от эксперимента и применить ту стратегию Х*, для которой достигается этот самый минимальный средний риск.

Пример 4.    Рассматривается игра с природой (табл. 9).

Определим, является ли целесообразным “идеальный” эксперимент, стоимость которого cost=2.

Таблица 9                                                                             

Матрица решений для примера 4

Решение. Перейдем к матрице рисков:

Таблица 10                            

Матрица рисков для примера 4

Минимальный средний риск равен 1.6, а стоимость эксперимента Cost=2, следовательно, эксперимент нецелесообразен. В качестве наилучшей следует принять альтернативу Х₁.

Неидеальный эксперимент

Теперь рассмотрим неидеальный эксперимент e, который не выясняет точно состояния a_j, а дает какие-то косвенные свидетельства в пользу тех или иных состояний.

Предположим, что эксперимент e приводит к появлению одного из B_k несовместных событий В₁, В₂,…, В_k:

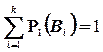 , причем вероятности событий a_j зависят от условий, в которых они проводятся.

Обозначим условную вероятность события B_l в условиях a_j  P(B_l/a_j) и будем считать, что она нам известна. После осуществления эксперимента e, давшего исход B_l, придется пересмотреть вероятности условий: состояния природы a_j будут характеризоваться не прежними (априорными) вероятностями, а новыми, апостериорными:  

- это условные вероятности событий a_j, они подсчитываются по известной формуле Байеса     

при условии, что эксперимент дал результат B_l. Этот подход к принятию решений в условиях неопределенности называется байесовским. В результате мы можем получить новую оптимальную стратегию.

    Рассмотрим предыдущий пример (табл. 6) с неидеальным экспериментом, который имеет три возможных исхода: B₁, B₂, B₃. Их условные вероятности приведены в табл. 8:

                                                                                                                                   Таблица 11       

Матрица условных вероятностей исходов

Известно, что в эксперименте имеет место исход B_1.  Вычислить апостериорные вероятности и найти оптимальное решение.

Решение. Вычислим апостериорные вероятности по формуле Байеса:

P₁₁= P₁*P(B₁/a₁) /

P₂₁=0.392

P₃₁=0.435

P₄₁=0.130

Тогда средний выигрыш равен , т.е.  (4.9; 5.20; 5.09), - следует выбрать альтернативу с максимальным результатом, т.е. Х₂.

Если бы выпал исход B₂, то можно посчитать все р_j2 и найти  (при этом средний выигрыш равен 5.53).