Основные положения теории принятия решений. Принятие решений в условиях неопределенности природы. Принятие решения при неопределенности целей. Принятие решений в условиях конфликта, страница 28

Как же найти смешанные стратегии игроков?

Если хотя бы у одного игрока число стратегий не превышает двух, то такие игры могут быть решены аналитически.

4.5 Решение игр 2х2

Пусть матрица игры, или платежная матрица А=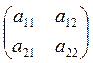, и пусть в игре нет седловой точки (иначе она бы решалась очень просто). Тогда решение игры будем искать в смешанных стратегиях: P=(p₁,p₂) -  для первого игрока и Q=(q₁,q₂) – для второго. Это значит, что первый игрок будет применять свою первую стратегию х₁ с вероятностью р₁, а свою вторую стратегию х₂ – с вероятностью р₂, причем р₁+р₂=1. Аналогично для второго игрока. Решим эту игру в общем виде с точки зрения второго игрока. Перепишем матрицу игры в следующем виде:

Найдем средний проигрыш второго игрока:

а₁₁×q₁+a₁₂×q₂=n - при первой стратегии первого игрока,

а₂₁×q₁+a₂₂×q₂=n, - при второй стратегии первого игрока,-

и решим эту систему, вычитая второе уравнение из первого:

(а₁₁-а₂₁)×q₁+(a₁₂-а₂₂)×q₂=0,    затем, учитывая, что q₂=1-q₁,   получим

(а₁₁-а₂₁-а₁₂+а₂₂)×q₁+(a₁₂-а₂₂)=0. 

Отсюда q₁=(a₂₂-а₁₂)/(а₁₁-а₂₁-а₁₂+а₂₂). Подставляя это значение q₁ в любое из уравнений, получим значение цены игры n.

С точки зрения первого игрока игра решается аналогично, только вычисляется уже средний выигрыш первого игрока:

а₁₁×p₁+a₂₁×p₂=n - при первой стратегии второго игрока, а₁₂×p₁+a₂₂×p₂=n,- при второй стратегии второго игрока.

Дальше решаем систему уравнений любым способом.

Вернемся к примеру 2. Матрица игры А=. Составим систему уравнений для второго игрока:

6q₁+2q₂=n

4q₁+8q₂=n, - решая совместно, получим  2q₁-6(1-q₁)=0, или 8q₁=6, или q₁=3/4.  Отсюда  Q=(3/4,1/4). Цена игры n=6×3/4+2×1/4=5Î[4,6]. Найдем оптимальную стратегию первого игрока. Поскольку цена игры уже известна, то достаточно написать только одно уравнение для среднего выигрыша первого игрока:

6p₁+4p₂=5, p₂=1-p₁, после подстановки получим 2p₁+4=5, откуда р₁=1/2. Следовательно, Р=(1/2,1/2).

Ответ: P=(1/2,1/2), Q=(3/4,1/4), n=5.

Систему уравнений, описывающих средний выигрыш первого игрока или средний проигрыш второго, можно решить также методом Крамера.

В примере 2 матрица А=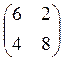, ее определитель ½А½=6×8-4×2=40. Тогда q₁=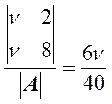, q₂==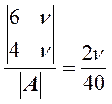. Поскольку q₁+q₂=1, то из 8n/40=1 следует n=5, а значит Q={3/4;1/4}. Вероятности P можно найти аналогично, но из транспонированной матрицы А*=, тогда p₁=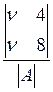=4n/40=1/2, учитывая, что цена игры уже определена (n=5), т.е. P={1/2;1/2}. 

4.6 Решение игр 2´n и m´2

Игры, где хотя бы у одного игрока две стратегии, можно решить аналитически. Если второй игрок имеет больше двух стратегий, то игра решается графо-аналитическим способом.

Рассмотрим игру 2´n: у первого игрока 2 стратегии, у второго игрока - n стратегий. Если в игре нет седловой точки, то будем искать решение игры в смешанных стратегиях. Решаем игру с точки зрения того игрока, у которого две стратегии.

Пусть Р=(р₁, р₂) – смешанная стратегия 1-го игрока, p₁+p₂=1;

Q= (q₁, q₂, ¼, q_n) – смешанная стратегия  2-го игрока.

Матрица игры   . Рассмотрим средний выигрыш первого игрока (у него две стратегии):

n₁ = a₁₁ p₁+a₂₁ p₂= a₂₁+(a₁₁-a₂₁)p₁  - при первой стратегии II игрока,

n₂ = a₁₂ p₁+a₂₂ p₂=a₂₂+(a₁₂-a₂₂)p₁  -  при второй стратегии II игрока и т.д.

Гарантированный результат первого игрока    n = max min{a_2j+(a_1j –a_2j)p₁}.

Линейные функции n₁, n₂,…,n_n   отражают зависимость среднего выигрыша первого игрока от вероятности применения им своей первой стратегии при различных стратегиях второго игрока. Поэтому для анализа ситуации необходимо изобразить их графически в осях n_I – p₁, имея в виду, что областью определения функций n₁, n₂,…,n_n   является интервал [0,1].

Чтобы обеспечить себе гарантированный результат, первый игрок должен выделить нижнюю границу среднего выигрыша при любой стратегии второго игрока. А затем найти максимальное значение среднего результата на этой границе. Соответствующая абсцисса равна вероятности применения первым игроком его первой стратегии, а ордината равна цене игры.