Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 9

Тому якщо E_k>0, то крива має більш високу і «гостру» вершину.

Якщо Е_k<0, то теоретично крива має більш низьку і «плоску» вершину. При цьому вважають, що математичне сподівання і дисперсія однакові для нормального закону розподілу і теоретичного розподілу.

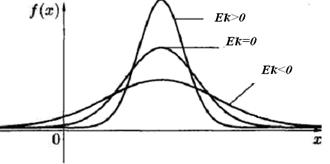
Рисунок 3.5 – Залежність  форми кривої розподілу  від

значення Е_k

3.2 Розподіл χ² (розподіл Пірсона)

Нехай маємо n незалежних випадкових величин x₁, x₂, ..., x_n, розподілених за нормальним законом з математичним сподіванням, що дорівнює нулю, і дисперсією, що дорівнює одиниці. Тоді випадкова величина

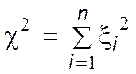
розподілена за законом, що називається “розподіл c²” або “розподіл Пірсона”. Очевидно, що вона може набирати лише невід’ємні значення. Число n називається числом ступенів вільності, χ² – розподіл залежить тільки від n.

При n > 1 графік щільності розподілу випадкової величини c² являє собою криву, зображену на рис. 3.6.

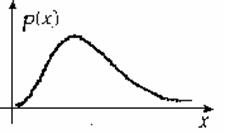
Рисунок 3.6 – Графік  щільності розподілу c²

Зі зростанням числа ступенів вільності n розподіл наближається до нормального закону розподілу (при n > 30 розподіл практично не відрізняється від нормального).

Математичне сподівання М(X)= n, дисперсія дорівнює 2n.

На практиці, як правило, використовують не щільність ймовірності, а квантилі розподілу. Квантилем розподілу c², що відповідає рівню значущості a, називається таке значення c_a², при якому

P(c² > c_a²) = a.

Ця формула означає: ймовірність того, що випадкова величина c²набере значення більше, ніж визначене значення c_a²,  дорівнює a.

Значення квантилів наводяться у спеціальних таблицях-додатках.

Таблиця 3.1 являє собою фрагмент таблиці розподілу c². З нього видно, що випадкова величина c² з десятьма ступенями вільності з ймовірністю α = 0,95 набирає значення більше, ніж 3,94, а та ж величина з одним ступенем вільності з ймовірністю α = 0,975 перевищує значення 0,00098.

Таблиця 3.1 – Фрагмент  таблиці розподілу c²

α  n	0,99	0,975	0,95	...	0,1	0,05	0,01
1	0,0315	0,0398	0,0239	...	2,71	3,84	6,63
...	...	...	...	...	...	...	...
10	2,56	3,25	3,94	...	16,0	18,3	23,2
...	...	...	...	...	...	...	...

Функції Excel

Для роботи з розподілом Пірсонаможна використовувати такі функції ( P(χ²>χ²_a)=a).

XИ2PACП(χ²_α; ступені_вільності) – повертає ймовірність α.

XИ2ОБP(ймовірність; ступені_вільності) – повертає значення χ²_α.

3.3 Розподіл Стьюдента (t – розподіл)

Багато задач статистики призводять до випадкової величини вигляду

,

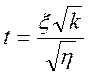де x і h – незалежні випадкові величини, причому x – нормально розподілена випадкова величина з параметрами
Mx = 0 і Dx = 1, а h  розподілена за законом c² c k  ступенями вільності.

Закон розподілу випадкової величини t називається законом розподілу Стьюдента з k ступенями вільності.

Графік щільності розподілу для закону Стьюдента схематично зображений на рисунку 3.7. Крива щільності розподілу схожа з аналогічною кривою для нормального розподілу.

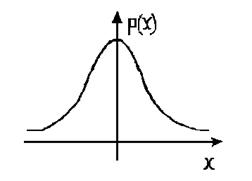
Рисунок 3.7 – Крива  щільності розподілу Стьюдента

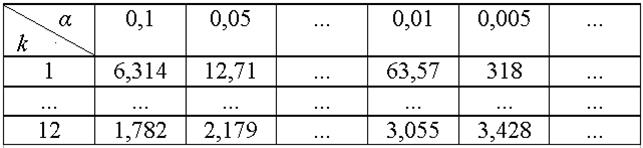
Таблиці розподілу Стьюдента дозволяють при даному числі ступенів вільності k за ймовірністю α визначити значення t_q, для якого виконується співвідношення P(|t| > t_q) = α. Фрагмент такої таблиці являє собою таблиця 3.2.

Таблиця 3.2 – Фрагмент  таблиці розподілу Стьюдента

В Excelдля роботи з розподіломСтьюдента можна використовувати такі функції:

СТЬЮДРАСП(х_a; ступені_вільності; ознака) – повертає ймовірність a, що є розв’язком рівняння ,
де  х_a – значення, для якого обчислюється розподіл Стьюдента; ступені_ вільності – число ступенів вільності, що характеризує розподіл; ознака – число сторін розподілу, що повертаються. Якщо ознака = 1, то функція СТЬЮДРАСП повертає однобічний розподіл. Якщо ознака = 2, то функція СТЬЮДРАСП повертає двосторонній розподіл.