Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 30

Нехай вихідна система складається з m ознак. Можна вивчати залежності між двома з них при фіксованому значенні  l  ознак з m-2, що залишилися. Розглянемо систему з 4 ознак, будемо вивчати залежність між X₂ і X₃ при фіксованому значенні  X₄. У цьому випадку маємо частковий коефіцієнт першого порядку. Якщо ми зафіксуємо значення X₁ і X₄  при вивченні залежності між X₂ і X₃, то одержимо частковий коефіцієнт другого порядку.

Формула вибіркового часткового коефіцієнта l-го порядку (l=m-2) має вигляд

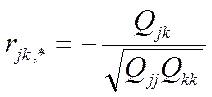,                          (6.6)

де Q_jk,Q_jj, Q_kk – алгебраїчні доповнення до відповідних елементів кореляційної матриці Q (6.5).

Для випадку, коли на змінну Y  діють 2 фактори X₁ і X₂, часткові коефіцієнти кореляції можна обчислити за  формулами:

 ,    ,

 .

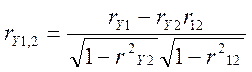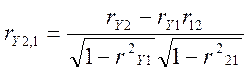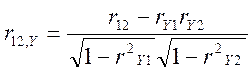Формулу вибіркового часткового коефіцієнта кореляції можна виразити не тільки через алгебраїчні доповнення кореляційної матриці Q, а й через елементи матриці Z, оберненої до матриці Q. Якщо чисельник і знаменник правої частини (6.6) розділити на визначник  кореляційної матриці  Q, то одержимо

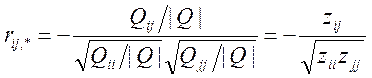,             (6.7)

де z_ij, z_ii, z_jj - елементи матриці Z=Q^-1.

Формула (6.7) особливо зручна, якщо на ЕОМ можна використати підпрограму, що обчислює обернену матрицю.

Значущість часткових коефіцієнтів кореляції оцінюють так само, як і для парних (6.3) , але число ступенів вільності

k=(n-l )-2 .

6.2.2 Множинний коефіцієнт  кореляції

Множинний коефіцієнт  кореляції дозволяє оцінити зв'язок однієї з ознак з усіма іншими.

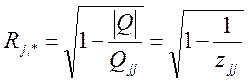,                 (6.8)

де |Q | – визначник кореляційної матриці,

Q_jj –  алгебраїчне доповнення до відповідного елемента кореляційної матриці,

 z_jj – елементи матриці Z=Q ^-1.

Квадрат коефіцієнта множинної кореляції називають множинним коефіцієнтом детермінації. Коефіцієнти множинної кореляції й детермінації - величини додатні і набувають значення з відрізку [0;1]. Чим ближче їх значення до 1, тим тісніший зв'язок результативної ознаки з усім набором досліджуваних факторів.

Приклад. За даними річних звітів десяти (n=10) підприємств провести аналіз залежності собівартості товарної продукції Y (ум. од.) від обсягу валової продукції X₁ (млн. ум. од.) і продуктивності праці X₂ (тис. ум. од. на чол.). Дані наведені в таблиці 6.2.

Таблиця 6.2 – Собівартість товарної продукції, обсяг валової продукції і продуктивність праці

№	Х1, (млн. ум. од.)	Х2, (тис. ум. од. на чол.).	Y, (ум. од.)	№	Х1, (млн. ум. од.)	Х2, (тис. ум. од. на чол.).	Y, (ум. од.)
1	3	1,8	2,1	6	5	1,5	4,9
2	4	1,5	2,8	7	6	1,6	5,5
3	5	1,4	3,2	8	7	1,2	6,5
4	5	1,3	4,5	9	15	1,3	12,1
5	5	1,3	4,8	10	20	1,2	15

1  Знаходимо матрицю парних коефіцієнтів кореляції за допомогою Сервис – Анализ данных – Корреляция.

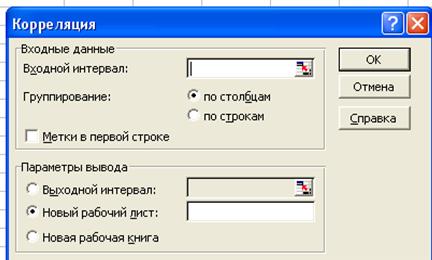
Вхідний діапазон. Посилання на діапазон, що містить аналізовані дані. Посилання повинно складатися не менш ніж із двох суміжних діапазонів даних, які розміщені у рядках або стовпчиках.

Групування. Встановіть перемикач у положення По столбикам  або По строкам залежно від  розміщення даних у вхідному діапазоні.

Мітки в першому рядку/Мітки в першому стовбці

Якщо перший рядок вхідного діапазону містить назви стовпців, встановіть перемикач у положення „Мітки в першому рядку”. Якщо назви рядків перебувають у першому стовпці вхідного діапазону, встановіть перемикач у положення „Мітки в першому стовпці”. Якщо вхідний діапазон не містить міток, то необхідні заголовки у вихідному діапазоні будуть створені автоматично.

Натисніть кнопку ОК. Отримаємо таку таблицю: