Нехай потрібно вивчити сукупність однорідних об'єктів щодо деякої якісної або кількісної ознаки (якщо є партія деталей: якісний – відповідність стандарту, кількісний – контрольований розмір).
Іноді проводять суцільне обстеження, тобто досліджується кожен об'єкт. На практиці таке обстеження застосовується порівняно рідко. Якщо обстеження пов'язане зі знищенням об'єкта або вимагає великих матеріальних витрат, то проводити суцільне обстеження немає сенсу. У таких випадках із усієї сукупності випадково відбирають обмежене число об'єктів і піддають їх вивченню.
Вибіркою називають сукупність випадково відібраних об'єктів.
Генеральною сукупністю називають сукупність об'єктів, з яких проводиться вибірка.
Для побудови адекватної стохастичної моделі нам необхідно визначити закон розподілу та його основні параметри для генеральної сукупності на основі інформації, отриманої з аналізу вибірки.
Метод статистичного дослідження, який полягає в тому, що на основі вивчення вибіркової сукупності робиться висновок про всю генеральну сукупність, називається вибірковим.
Для одержання достовірних оцінок характеристик генеральної сукупності необхідно, щоб вибірка була репрезентативною (або представницькою), тобто вона повинна досить повно представляти досліджувані ознаки генеральної сукупності. Умовою забезпечення репрезентативності вибірки є відповідно до закону великих чисел дотримання випадковості відбору, тобто всі об'єкти генеральної сукупності повинні мати рівні ймовірності потрапити у вибірку.
На практиці часто буває так, що вигляд закону відомий заздалегідь, тому задача зводиться до визначення невідомих параметрів, їх оцінки за обмеженим числом вимірювань.
Для визначення вигляду закону і його параметрів необхідно виконати ряд дій, пов’язаних з аналізом отриманих даних.
Нехай вивчається якась випадкова величина X. Із цією метою над випадковою величиною X проводять ряд незалежних спостережень. У кожному з цих випробувань величина X набирає те або інше значення.
Нехай вона прийняла n1 разів значення х1, n2 разів - значення х2,..., nк разів – значення хк. При цьому n1+ n2+...+ nк = n – обсяг вибірки. Значення х1, х2,..., хк називаються варіантами випадкової величини X.
Вся сукупність значень випадкової величини X являє собою первинний статистичний матеріал, що підлягає подальшій обробці, насамперед упорядкуванню.
Операція розташування значень випадкової величини (ознаки) за неспаданням називається ранжуванням статистичних даних.
Отримана в такий спосіб послідовність х1,х2,…xn значень випадкової величини X (де х1≤х2≤…≤хп та x1 = min1≤і≤пХі, … хп = max1≤і≤пХі) називається варіаційним рядом.
Числа пі, що показують, скільки разів зустрічаються варіанти xі у ряді спостережень, називаються частотами, а відношення їх до обсягу вибірки – відносними частотами (рі*), тобто
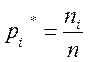 , де
, де 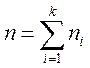 .
.
Перелік варіантів і відповідних їм частот або частостей називається статистичним розподілом вибірки або статистичним рядом.
4.3.1 Статистичний розподіл у вигляді таблиці
Записується статистичний розподіл у вигляді таблиці. Перший рядок містить варіанти, а другий – їх частоти nі (або частості рі*).
Статистичний розподіл вибірки є оцінкою невідомого розподілу. Відповідно до теореми Бернуллі відносні частоти рі* сходяться при п → ∞ до відповідних ймовірностей pі. Тому при великих значеннях n статистичний розподіл мало відрізняється від розподілу випадкової величини.
У випадку, коли число значень ознаки X велике або ознака є неперервною, складають інтервальний статистичний ряд. У перший рядок таблиці статистичного розподілу вписують часткові проміжки [х0,х1), [х1,х2),..., [xk-і,хк), які беруть звичайно однаковими по довжині: h = х1- x0 = x2-х1=... Для визначення величини інтервалу (h) можна використати формулу Стерджеса
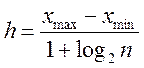 ,
,
де – log2 n ≈ 3,322 lg n.
За початок першого інтервалу рекомендується брати величину хпоч=хmіn-h/2. У другий рядок статистичного ряду вписують кількість спостережень ni,, що потрапили в кожний інтервал.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.